在求解过程中,依据某种贪心标准,从问题的初始状态出发,直接去求每一步的最优解,通过若干次的贪心选择,最终得出整个问题的最优解。
从贪心算法的定义可以看出,贪心算法不是从整体上考虑问题,它所做出的选择只是在某种意义上的局部最优解,而由问题自身的特性决定了该题运用贪心算法可以得到最优解。如果一个问题可以同时用几种方法解决,贪心算法应该是最好的选择之一。
(1)最优子结构性质
(2)贪心选择性质(局部最优选择)
1、活动安排
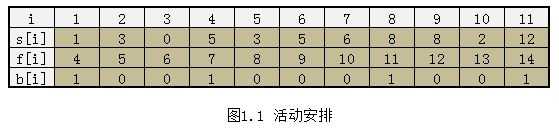
设有n个活动的集合 E = {1,2,…,n},其中每个活动都要求使用同一资源,如演讲会场等,而在同一时间内只有一个活动能使用这一资源。
每个活动 i 都有一个要求使用该资源的起始时间 si 和一个结束时间 fi,且 si < fi。如果选择了活动i,则它在半开时间区间 [si ,fi ) 内占用资源。若区间 [si , fi )与区间 [sj, fj ) 不相交,则称活动i与活动j是相容的。当 si ≥ fj 或 sj ≥ fi 时,活动 i 与活动 j 相容。
活动安排问题就是在所给的活动集合中选出最大的相容活动子集合。
例如:
1 #include <iostream> 2 using namespace std; 3 4 #define NUM 50 5 6 void GreedySelector(int n, int s[], int f[], bool b[]) 7 { 8 b[1]=true; //默认将第一个活动先安排 9 int j=1; //记录最近一次加入b中的活动 10 11 //依次检查活动i是否与当前已选择的活动相容 12 for(int i=2;i<=n;i++) 13 { 14 if (s[i]>=f[j]) 15 { 16 b[i]=true; 17 j=i; 18 } 19 else 20 b[i]=false; 21 } 22 } 23 24 int main() 25 { 26 int s[] = {0,1,3,0,5,3,5,6,8,8,2,12}; //存储活动开始时间 27 int f[] = {0,4,5,6,7,8,9,10,11,12,13,14}; //存储活动结束时间 28 bool b[NUM]; //存储被安排的活动编号 29 int n = (sizeof(s) / sizeof(s[0])) - 1; 30 31 GreedySelector(n, s, f, b); 32 33 for(int i = 1; i <= n; i++) //输出被安排的活动编号和它的开始时间和结束时间 34 { 35 if(b[i]) cout << "活动 " << i << " :" << "(" << s[i] << "," << f[i] << ")" <<endl; 36 } 37 return 0; 38 }
2、背包问题
给定一个载重量为 M 的背包,考虑 n 个物品,其中第 i 个物品的重量 wi(1 ≤ i ≤ n),价值 vi(1 ≤ i ≤ n),要求把物品装满背包,且使背包内的物品价值最大。
有两类背包问题(根据物品是否可以分割),如果物品不可以分割,称为 0—1 背包问题(动态规划);如果物品可以分割,则称为背包问题(贪心算法)。
例如:
有3种方法来选取物品:
(1)当作 0—1 背包问题,用动态规划算法,获得最优值 220;
(2)当作 0—1 背包问题,用贪心算法,按性价比从高到底顺序选取物品,获得最优值 160。由于物品不可分割,剩下的空间白白浪费。
(3)当作背包问题,用贪心算法,按性价比从高到底的顺序选取物品,获得最优值 240。由于物品可以分割,剩下的空间装入物品 3 的一部分,而获得了更好的性能。
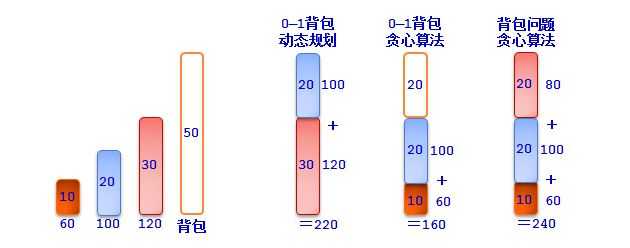
图2.1 背包问题
1 #include <iostream> 2 using namespace std; 3 4 #define NUM 50 5 6 //这里假设 w[], v[] 已按要求排好序 7 void Knapsack(int n,float M,float v[],float w[],float x[]) 8 { 9 int i; 10 for(i = 1; i <= n; i++) x[i] = 0; //初始化数组 11 float c = M; 12 for(i = 1;i <= n; i++) //全部被装下的物品,且将 x[i] = 1 13 { 14 if(w[i]>c) break; 15 x[i] = 1; 16 c -= w[i]; 17 } 18 19 if(i <= n) x[i] = c / w[i]; //将物品i 的部分装下 20 } 21 22 int main() 23 { 24 float M = 50; //背包所能容纳的重量 25 float w[] = {0,10,20,30}; //这里给定的物品按价值降序排序 26 float v[] = {0,60,100,120}; 27 float x[NUM]; //存储每个物品装入背包的比例 28 29 int n = (sizeof(w) / sizeof(w[0])) - 1; 30 31 Knapsack(n, M, v, w, x); 32 33 for(int i = 1; i <= n; i++) 34 cout << "物品 " << i << " 装入的比例: " << x[i] << endl; 35 return 0; 36 }
原文:http://www.cnblogs.com/cao-lei/p/6896841.html