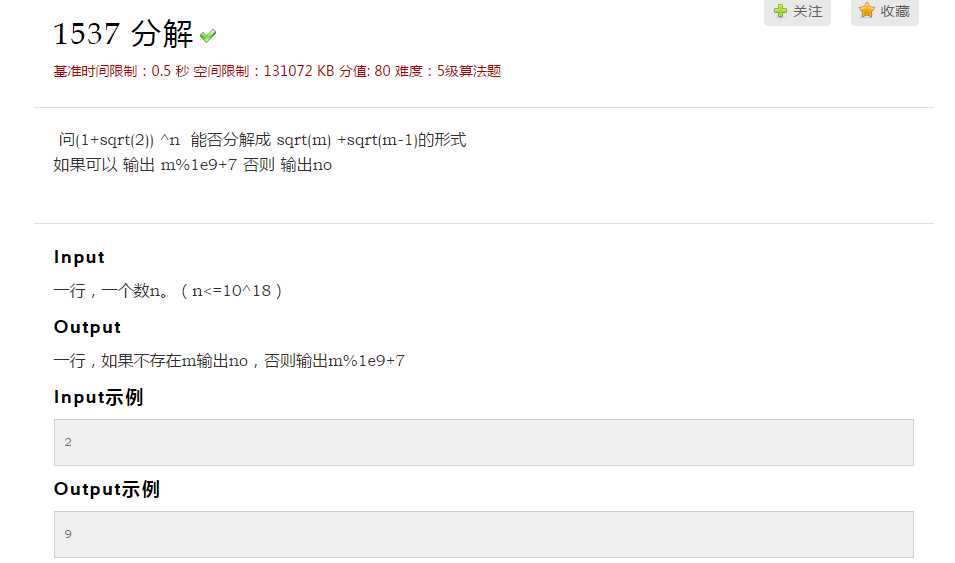
分析:先写出前几项,发现都是有解的.记(1+√2)^n=a+b√2,可以归纳证明,当n为奇数时,m=a^2+1,n为偶数时,m=a^2.写出a的递推式,用矩阵快速幂算一下a即可.
1 #include<iostream> 2 #include<cstring> 3 #include<cstdio> 4 using namespace std; 5 const int p=1e9+7; 6 typedef unsigned long long ull; 7 ull mat[2][2]={2,1,1,0}; 8 void Copy(ull a[2][2],ull b[2][2]){ 9 for(int i=0;i<2;i++) 10 for(int j=0;j<2;j++)a[i][j]=b[i][j]; 11 } 12 void multiple(ull result[2][2],ull a0[2][2],ull b0[2][2]){ 13 ull a[2][2],b[2][2]; 14 Copy(a,a0);Copy(b,b0); 15 for(int i=0;i<2;i++){ 16 for(int j=0;j<2;j++){ 17 result[i][j]=0; 18 for(int k=0;k<2;k++) 19 result[i][j]=(result[i][j]+a[i][k]*b[k][j])%p; 20 } 21 } 22 } 23 void qpow(ull t,ull ans[2][2]){ 24 ull y[2][2]; 25 Copy(y,mat); 26 ans[0][0]=ans[1][1]=1; 27 ans[0][1]=ans[1][0]=0; 28 ull k=1; 29 while(k){ 30 if(k&t){ 31 multiple(ans,ans,y); 32 } 33 multiple(y,y,y); 34 k<<=1; 35 } 36 } 37 int main(){ 38 ull n; 39 cin>>n; 40 if(n==0)cout<<1<<endl; 41 else if(n==1)cout<<2<<endl; 42 else{ 43 ull a[2][2]; 44 qpow(n-1,a); 45 ull t=((a[0][0]+a[1][0])*(a[0][0]+a[1][0]))%p; 46 if(n%2)cout<<t+1<<endl; 47 else cout<<t<<endl; 48 } 49 return 0; 50 }
原文:http://www.cnblogs.com/7391-KID/p/6914592.html