在一个 2^k * 2^k 个方格组成的棋盘中,若恰有一个方格与其他方格不同。则称该方格为一特殊方格,称该棋盘为一特殊棋盘。显然特殊方格在棋盘上出现的位置有 4^k 种情形。因而对不论什么 k>=0 。有 4^k 种不同的特殊棋盘。
下图所看到的的特殊棋盘为 k=2 时 16 个特殊棋盘中的一个。

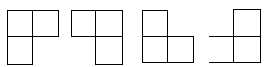
在棋盘覆盖问题中,要用下图中 4 中不同形态的 L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的全部方格,且不论什么 2 个 L 型骨牌不得重叠覆盖。
易知,在不论什么一个 2^k * 2^k 的棋盘中,用到的 L 型骨牌个数恰为 (4^k-1)/3 。
用分治策略,能够设计解棋盘问题的一个简捷的算法。
当 k>0 时,将 2^k * 2^k 棋盘切割为 4 个 2^(k-1) * 2^(k-1) 子棋盘,例如以下图所看到的。

特殊方格必位于 4 个较小子棋盘之中的一个中,其余 3 个子棋盘中无特殊方格。
为了将这 3 个无特殊方格的子棋盘转化为特殊棋盘,我们能够用一个 L 型骨牌覆盖这 3 个较小的棋盘的汇合处。例如以下图所看到的。这 3 个子棋盘上被 L 型骨牌覆盖的方格就成为该棋盘上的特殊方格,从而将原问题化为 4 个较小规模的棋盘覆盖问题。递归的使用 这样的切割。直至棋盘简化为 1x1 棋盘。
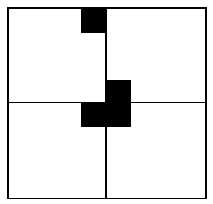

附代码:
<!DOCTYPE HTML PUBLIC "-//W3C//DTD HTML 4.0 Transitional//EN">
<HTML>
<HEAD>
<TITLE> New Document </TITLE>
<META NAME="Generator" CONTENT="EditPlus">
<META NAME="Author" CONTENT="">
<META NAME="Keywords" CONTENT="">
<META NAME="Description" CONTENT="">
<script type="text/javascript" src="jquery-1.7.2.min.js"></script>
<script type="text/javascript" src="json2.js"></script>
<style>
table,td{
border:1px solid gray;
text-align:center;
color:white;
}
</style>
<script>
var t=0;
var color_arr=[‘red‘,‘yellow‘,‘green‘,‘blue‘,‘purple‘,‘orange‘,‘pink‘];
var num
function initTable(){
$("#container").html(‘‘);
var table=$("<table></table>");
num=Math.pow(2,parseInt($("#txt_k").val()));
var width=document.body.clientWidth*0.4/num;
for(var i=0;i<num;i++){
var tr=$("<tr style=‘width:"+width*num+"px;height:"+width+"px;‘></tr>");
for(var j=0;j<num;j++){
var td=$("<td style=‘width:"+width+"px;height:"+width+"px;‘> </td>");
if(i==parseInt($("#txt_x").val())-1&&j==parseInt($("#txt_y").val())-1)
td.css("background-color","black");
tr.append(td);
}
table.append(tr);
}
$("#container").append(table);
}
function calcTable(){
var dr=parseInt($("#txt_x").val())-1;
var dc=parseInt($("#txt_y").val())-1;
t=0;
chessBoard(0,0,dr,dc,num);
}
//tr tc子棋盘左上角坐标 dr dc特殊格子坐标 size子棋盘格子数
function chessBoard(tr,tc,dr,dc,size){
var s,t1;
if(size==1)
return;
t1=++t;
s=size/2;
var color=color_arr[t1%color_arr.length];
//-------------左上角子棋盘-----------------
if(dr<tr+s&&dc<tc+s){
//特殊格子在右上角,递归处理子棋盘
chessBoard(tr,tc,dr,dc,s);
}else{
//处理右下角环绕切割点的棋盘
//标记特殊棋盘
$("table tr").eq(tr+s-1).find("td").eq(tc+s-1).text(t1);
$("table tr").eq(tr+s-1).find("td").eq(tc+s-1).css("background-color",color);
chessBoard(tr,tc,tr+s-1,tc+s-1,s);
}
//--------------右上角棋盘-------------------
if(dr>=tr+s&&dc<tc+s){
chessBoard(tr+s,tc,dr,dc,s);
}else{
//左下角格子
$("table tr").eq(tr+s).find("td").eq(tc+s-1).text(t1);
$("table tr").eq(tr+s).find("td").eq(tc+s-1).css("background-color",color);
chessBoard(tr+s,tc,tr+s,tc+s-1,s);
}
//--------------左下角棋盘-------------------
if(dr<tr+s&&dc>=tc+s){
chessBoard(tr,tc+s,dr,dc,s);
}else{
$("table tr").eq(tr+s-1).find("td").eq(tc+s).text(t1);
$("table tr").eq(tr+s-1).find("td").eq(tc+s).css("background-color",color);
chessBoard(tr,tc+s,tr+s-1,tc+s,s);
}
//--------------右下角棋盘-------------------
if(dr>=tr+s&&dc>=tc+s){
chessBoard(tr+s,tc+s,dr,dc,s);
}else{
//setTimeout("setColor("+tr+s+","+tc+s+",‘"+color+"‘)",1000);
$("table tr").eq(tr+s).find("td").eq(tc+s).text(t1);
$("table tr").eq(tr+s).find("td").eq(tc+s).css("background-color",color);
chessBoard(tr+s,tc+s,tr+s,tc+s,s);
}
}
</script>
</HEAD>
<BODY style="text-align:center">
<div>
级数:
<input type="text" id="txt_k"/>
坐标X:
<input type="text" id="txt_x"/>
坐标Y:
<input type="text" id="txt_y"/>
<input type="button" id="btn" value="初始化表格" onclick="initTable()"/>
<input type="button" id="btn" value="開始棋盘覆盖" onclick="calcTable()"/>
</div>
<div id=‘container‘ style="margin:0 auto;">
</div>
</BODY>
</HTML>
原文:http://www.cnblogs.com/blfbuaa/p/6916706.html