2.深度优先搜索
为了访问一个顶点,我们将它标记为已经访问过,然后递归的访问所有与子邻接的并且尚未标记的顶点,这就是深度优先搜索(DFS),DFS常用于解决路径问题。
比如下面的连通图,我们从顶点0开始对图进行探索
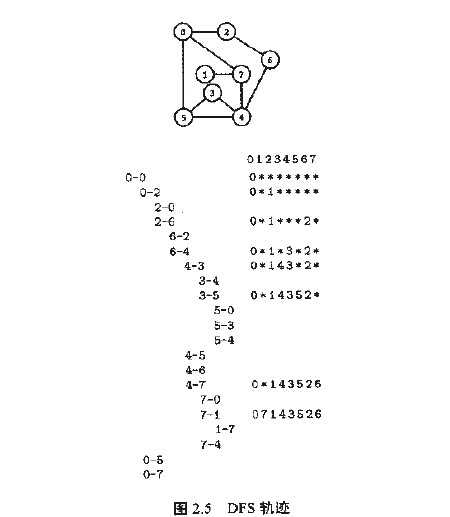
下面这个图显示了DFS处理时的递归调用树。
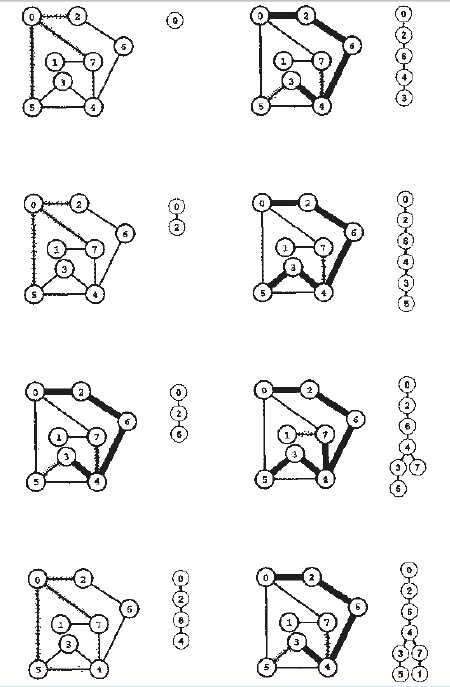
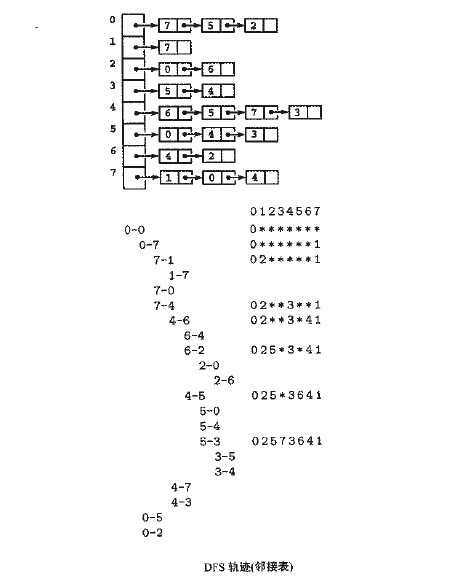
DFS可以解决的问题:
1)环检测:一个图中有环吗?该图是森林吗?
2)简单路径:给定两个顶点,是否存在一条连接他们的路径
3)简单连通性:无论何时使用DFS,都可以在线性时间内确定一个图是否连通
4)顶点搜索:在给定顶点所在的同一个连通分量中有多少个顶点呢?
DFS算法的特点:
1)对于用邻接矩阵表示的图,其DFS需要的时间与V*V成正比
2)对于用邻接表表示的图,其DFS需要的时间与V+E成正比
1 //程序:连通分量的深度优先搜索 2 #include <vector> 3 template <class Graph> class cDFS 4 { 5 private: 6 int cnt;//记录搜索顺序的变量 7 const Graph& G; 8 vector<int> order;//保存每个顶点被搜索的顺序 9 void serachC(int v) 10 { 11 order[v]=cnt++; 12 typename Graph::adjIterator ite(G,v);//图的迭代器,上一节有介绍过 13 for(int t=ite.begin();!ite.end();t=ite.next()) 14 if(order[t]==-1) serachC(t);//如果顶点未被标记,递归调用搜索函数 15 16 } 17 public: 18 cDFS(const Graph& g,int v=0):G(g),cnt(0),order(g.V(),-1){ 19 serachC(v); 20 } 21 int count() const{return cnt;}//返回图的顶点数 22 int operator[](int v) const{return order[v];} 23 24 };
3.广度优先搜索
假设希望找到一个图中两个特定顶点之间的一条最短路径--连接这两个顶点并且满足:在连接这两个顶点的路径中,不存在边数笔它更少的其他路径,这里我们使用广度优先搜索(BFS),在进行图搜索时,会有多条边可以遍历,可先选择其中一条,并保存其他边留待后续处理,我们这里需要使用一个先进先出队列,然后按下列步骤处理,直到队列为空:
1)从队列中pop一个顶点
2)访问该顶点,将由此顶点到未访问顶点的所有边放入队列中
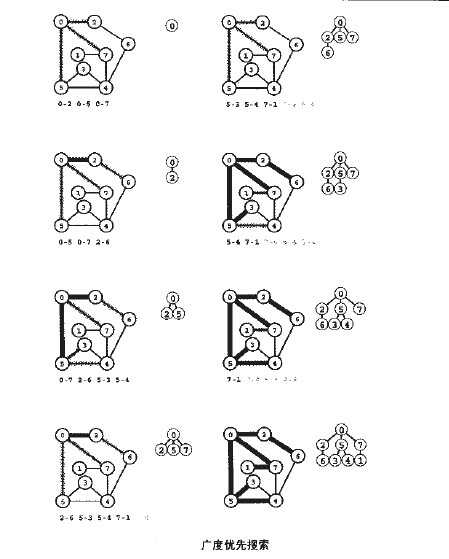
1 //程序:广度优先搜索单源最短路径 2 #include <queue> 3 4 template <class Graph> class BFS 5 { 6 private: 7 const Graph& G; 8 vector<int> dist;//用来存储每个顶点和源点的距离 9 vector<int> path;//用来存储每个顶点的前一个顶点 10 void search(int s) 11 { 12 queue<int> q; 13 q.push(s); 14 while(!q.empty()) 15 { 16 int v=q.pop(); 17 typename Graph::adjIterator ite(G,v);//邻接表迭代器 18 for(int w=ite.begin();!ite.end();w=ite.next()) 19 20 if(dist[w]==-1) 21 { 22 dist[w]=dist[v]+1; 23 path[w]=v; 24 q.push(w); 25 } 26 27 } 28 } 29 public: 30 BFS(const Graph& g,int s):G(g),dist(g.V(),-1),path(g.V(),0){search(s);} 31 int distance(int v) const{return dist[v];} 32 int path(int v) const{return path[v];} 33 34 };
在BFS中,顶点以其与起始顶点的距离为顺序进入和离开FIFO顺序,如下图所示:
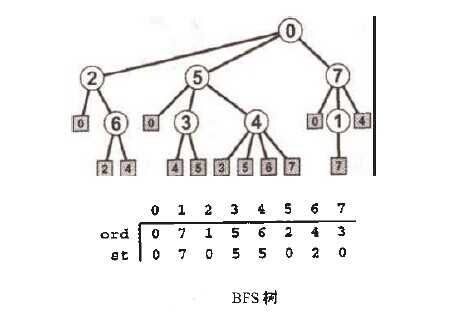
在以s为根的BFS树中,对于其中任何一个节点w,从v到w的数路径对应为图中从v到w的最短路径,如下图所示:
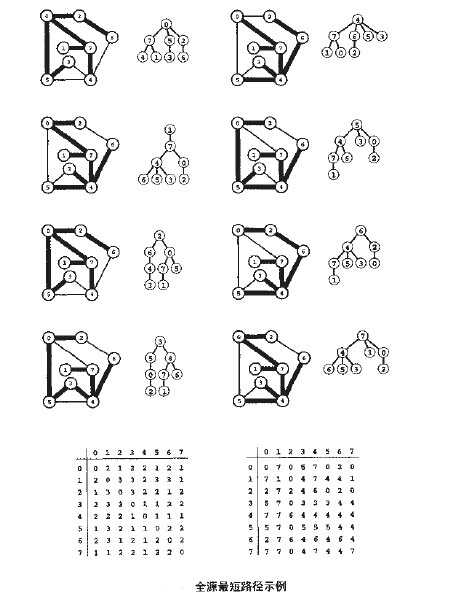
利用BFS可以解决最短路径,单源最短路径和全源最短路径的问题。
图算法系列-深度优先搜索与广度优先搜索,布布扣,bubuko.com
原文:http://www.cnblogs.com/lippi/p/3774927.html