hdu1394 树状数组 解法

本题使用树状数组果然更加快。

树状数组难点：

1 如何遍历树

2 如何利用数组数据

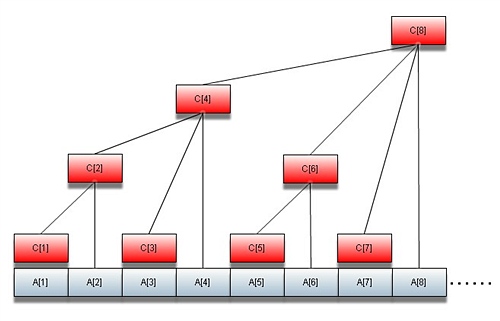
建立一个树状数组就如上图红色部分代表所有的树状数组节点了。

基本操作：

查找下一个节点的计算，如不明白下面函数的作用，请查看负数内存存放的问题。

简而言之就是：内存放是求反+1； 利用这个函数可以神奇地寻找到其单亲节点和兄弟节点，比如上图6->8，6->4或者7->8， 7 -> 6这样跳转节点。

这是树状数组实现的关键了，理解了如何遍历这样的树，就会使用这个数据结构了。

inline int lowbit(int x)
	{
		return x & (-x);//or return x&(x^(x-1));
	}

void update(int i, int val, int len)
	{
		while (i <= len)
		{
			c[i] += val;
			i += lowbit(i);
		}
	}

int getsum(int x)
	{
		int ans = 0;
		while (x > 0)
		{
			ans += c[x];
			x -= lowbit(x);
		}
		return ans;
	}

参考资料：

http://www.cppblog.com/Ylemzy/articles/98322.html

解决这道题的代码：

class MinimumInversionNumber_3_TreeArray
{
	static const int SIZE = 5005;
	int *a, *c;//一般数组和树状数组
	inline int lowbit(int x)
	{
		return x & (-x);//or return x&(x^(x-1));
	}

	void update(int i, int val, int len)
	{
		while (i <= len)
		{
			c[i] += val;
			i += lowbit(i);
		}
	}

	int getsum(int x)
	{
		int ans = 0;
		while (x > 0)
		{
			ans += c[x];
			x -= lowbit(x);
		}
		return ans;
	}
public:
	MinimumInversionNumber_3_TreeArray() : a((int*)malloc(sizeof(int)*SIZE)), 
		c((int*)malloc(sizeof(int)*SIZE))
	{
		int n, t;  
		while(~scanf("%d",&n))  
		{
			for(int i = 1; i <= n; i++)
			{  
				scanf("%d", &t);  
				a[i] = t + 1;  
			}  

			//memset(c, 0, sizeof(c));最好不要使用memset设置初值
			fill(c, c+n+1, 0);
			int res = 0;  
			for(int i = 1; i <= n; i++)  
			{  
				update(a[i], 1, n);
				res += i - getsum(a[i]);//目前为止，出现了多少个小于等于a[i]的数位getsum(a[i])，所以大于a[i]的数位i-getsum(a[i])，即为逆序数
			}  
			int ans = res;
			for(int i = 2; i <= n; i++)  
			{  
				res += n - 2*a[i-1] + 1;  
				if(res < ans) ans = res;  
			}  
			printf("%d\n", ans);  
		}     
	}

	~MinimumInversionNumber_3_TreeArray()
	{
		free(a);
		free(c);
	}
};

hdu1394 树状数组 解法,布布扣,bubuko.com

hdu1394 树状数组 解法

原文：http://blog.csdn.net/kenden23/article/details/28891421