1. 饭后,姐姐洗碗,妹妹把姐姐洗过的碗一个一个地放进碗橱摞成一摞。一共有n个不同的碗,洗前也是摞成一摞的,也许因为小妹贪玩而使碗拿进碗橱不及时,姐姐则把洗过的碗摞在旁边,问:小妹摞起的碗有多少种可能的方式?
2. 给定n个数,有多少种出栈序列?
3. 一个有n个1和n个-1组成的字串,且前k个数的和均不小于0,那这种字串的总数为多少?
这三个问题具有相同的结构,三个问题是可以互相转化。将姐姐放碗看做入栈操作,将妹妹放碗看做出栈操作。则问题一变为问题二。将入栈操作记为1,出栈记为-1,问题2变为问题3。
问题的答案是一个著名的数列,卡特兰数。该问题的代数解法比较抽象,而运用到几何上,用图片来描述,却有让人恍然大悟的感觉。
一、递推
我们把n个元素的出栈个数的记为f(n), 那么对于1,2,3, 我们很容易得出:
f(1) = 1 //即 1
f(2) = 2 //即 12、21
f(3) = 5 //即 123、132、213、321、231
然后我们来考虑f(4), 我们给4个元素编号为a,b,c,d, 那么考虑:元素a只可能出现在1号位置,2号位置,3号位置和4号位置(很容易理解,一共就4个位置,比如abcd,元素a就在1号位置)。
分析:
1) 如果元素a在1号位置,那么只可能a进栈,马上出栈,此时还剩元素b、c、d等待操作,就是子问题f(3);
2) 如果元素a在2号位置,那么一定有一个元素比a先出栈,即有f(1)种可能顺序(只能是b),还剩c、d,即f(2), 根据乘法原理,一共的顺序个数为f(1) * f(2);
3) 如果元素a在3号位置,那么一定有两个元素比1先出栈,即有f(2)种可能顺序(只能是b、c),还剩d,即f(1),
根据乘法原理,一共的顺序个数为f(2) * f(1);
4) 如果元素a在4号位置,那么一定是a先进栈,最后出栈,那么元素b、c、d的出栈顺序即是此小问题的解,即 f(3);
结合所有情况,即f(4) = f(3) + f(2) * f(1) + f(1) * f(2) + f(3);
为了规整化,我们定义f(0) = 1;于是f(4)可以重新写为:
f(4) = f(0)*f(3) + f(1)*f(2) + f(2) * f(1) + f(3)*f(0)
然后我们推广到n,推广思路和n=4时完全一样,于是我们可以得到:
f(n) = f(0)*f(n-1) + f(1)*f(n-2) + ... + f(n-1)*f(0)
即
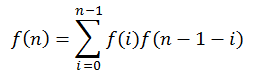
二、通项(卡特兰数)
C(2n,n)/(n+1)
事实上,可以认为问题是,任意两种操作,要求每种操作的总次数一样,且进行第k次操作2前必须先进行至少k次操作1。我们假设一个人在原点,操作1是此人沿右上角45°走一个单位(一个单位设为根号2,这样他第一次进行操作1就刚好走到(1,1)点),操作2是此人沿右下角45°走一个单位。第k次操作2前必须先进行至少k次操作1,就是说明所走出来的折线不能跨越x轴走到y=-1这条线上!在进行n次操作1和n此操作2后,此人必将到到达(2n,0)!若无跨越x轴的限制,折线的种数将为C(2n,n),即在2n次操作中选出n次作为操作1的方法数。
现在只要减去跨越了x轴的情况数。对于任意跨越x轴的情况,必有将与y=-1相交。找出第一个与y=-1相交的点k,将k点以右的折线根据y=-1对称(即操作1与操作2互换了)。可以发现终点最终都会从(2n,0)对称到(2n,-2)。由于对称总是能进行的,且是可逆的。我们可以得出所有跨越了x轴的折线总数是与从(0,0)到(2n,-2)的折线总数。而后者的操作2比操作1要多0-(-2)=2次。即操作1为n-1,操作2为n+1。总数为C(2n,n-1)。
原文:http://www.cnblogs.com/Xilian/p/3775750.html