Description
The crowdedness of the discotheque would never stop our friends from having fun, but a bit more spaciousness won‘t hurt, will it?
The discotheque can be seen as an infinite xy-plane, in which there are a total of n dancers. Once someone starts moving around, they will move only inside their own movement range, which is a circular area Ci described by a center (xi,?yi) and a radius ri. No two ranges‘ borders have more than one common point, that is for every pair (i,?j) (1?≤?i?<?j?≤?n) either ranges Ci and Cj are disjoint, or one of them is a subset of the other. Note that it‘s possible that two ranges‘ borders share a single common point, but no two dancers have exactly the same ranges.
Tsukihi, being one of them, defines the spaciousness to be the area covered by an odd number of movement ranges of dancers who are moving. An example is shown below, with shaded regions representing the spaciousness if everyone moves at the same time.
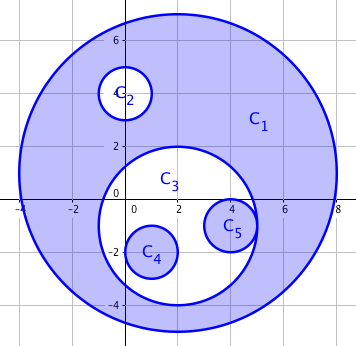
But no one keeps moving for the whole night after all, so the whole night‘s time is divided into two halves — before midnight and after midnight. Every dancer moves around in one half, while sitting down with friends in the other. The spaciousness of two halves are calculated separately and their sum should, of course, be as large as possible. The following figure shows an optimal solution to the example above.
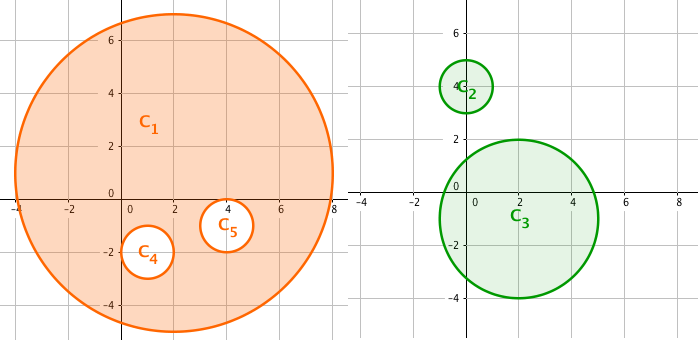
By different plans of who dances in the first half and who does in the other, different sums of spaciousness over two halves are achieved. You are to find the largest achievable value of this sum.
The first line of input contains a positive integer n (1?≤?n?≤?1?000) — the number of dancers.
The following n lines each describes a dancer: the i-th line among them contains three space-separated integers xi, yi and ri(?-?106?≤?xi,?yi?≤?106, 1?≤?ri?≤?106), describing a circular movement range centered at (xi,?yi) with radius ri.
Output one decimal number — the largest achievable sum of spaciousness over two halves of the night.
The output is considered correct if it has a relative or absolute error of at most 10?-?9. Formally, let your answer be a, and the jury‘s answer beb. Your answer is considered correct if 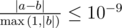 .
.
5
2 1 6
0 4 1
2 -1 3
1 -2 1
4 -1 1
138.23007676
8
0 0 1
0 0 2
0 0 3
0 0 4
0 0 5
0 0 6
0 0 7
0 0 8
289.02652413
The first sample corresponds to the illustrations in the legend.
题意:给出奇数个圆,分成两部分,使得阴影面积最大(只包含内含和内切)
解法:贪心,谁被谁包含,如果没有被包含的圆,说明它最大,加起来,如果被包含的圆为奇数个,加起来,如果被包含是偶数个,则减去
比如C1包含所有的圆,加起来,C2被C1包含,加起来,C3被C1包含,加起来,C4被C3和C1包含,减去,C5被C3和C1包含,减去
1 #include<iostream> 2 #include<cmath> 3 #include<cstring> 4 #include<cstdio> 5 #include<vector> 6 #include<stack> 7 #include<queue> 8 #include<algorithm> 9 #include<sstream> 10 #define inf 0x3f3f3f3f 11 #define ll long long 12 using namespace std; 13 double pi=acos(-1.); 14 struct P 15 { 16 double x,y; 17 double r; 18 double s; 19 } H[12345]; 20 struct Q 21 { 22 int x,y; 23 } HH[12345]; 24 double dis(double x1,double y1,double x2,double y2) 25 { 26 return sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)); 27 } 28 vector<int>q[12345]; 29 bool cmd(Q a,Q b) 30 { 31 return a.y>b.y; 32 // return x>y; 33 } 34 int main() 35 { 36 int n; 37 cin>>n; 38 for(int i=1; i<=n; i++) 39 { 40 cin>>H[i].x>>H[i].y>>H[i].r; 41 H[i].s=(H[i].r*H[i].r*pi); 42 } 43 double ANS=0.0; 44 int ans=0; 45 for(int i=1; i<=n; i++) 46 { 47 ans=0; 48 for(int j=1; j<=n; j++) 49 { 50 if(i!=j) 51 { 52 double sum=dis(H[i].x,H[i].y,H[j].x,H[j].y); 53 if(sum<=(H[j].r-H[i].r)) 54 { 55 q[i].push_back(j); 56 } 57 } 58 } 59 ans+=q[i].size(); 60 // printf("%d\n",ans); 61 if(ans==0||ans%2) 62 { 63 ANS+=H[i].s; 64 } 65 else 66 { 67 ANS-=H[i].s; 68 } 69 } 70 printf("%.15f\n",ANS); 71 return 0; 72 }
Codeforces Round #418 (Div. 2) D
原文:http://www.cnblogs.com/yinghualuowu/p/6965313.html