| Time Limit: 15000MS | Memory Limit: 150000K | |
| Total Submissions: 6396 | Accepted: 2153 |
Description
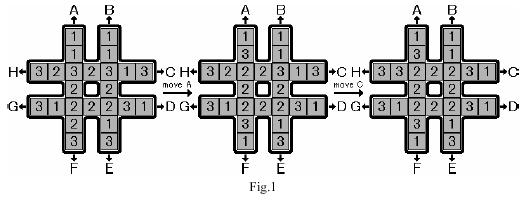
Input
Output
Sample Input
1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3 0
Sample Output
AC 2 DDHH 2
题目链接:POJ 2286
第一道IDA*题目,由于用的是递归的写法,代码量实际上不会很大,只要在dfs入口处做好各种判断就可以了 ,能用IDA*的前提至少答案要存在,如果不存在的话搜索深度会无限加深就没有意义了,然后每一次都用估价函数剪枝即可,再加一个防止来回的剪枝速度可以快一倍
大致伪代码如下:
void dfs(state, dep)
{
计算此时状态下的估价函数值h(state)
if(h(state)==0)
已到终点,返回true
else if(h(state)+dep>Maxdep)
在规定的Maxdep内一定走不到终点,返回false
else
{
for....
{
得到新状态n_state
if(dfs(n_state,dep))
return 1;
}
}
return 0;
}
代码:
#include <stdio.h>
#include <iostream>
#include <algorithm>
#include <cstdlib>
#include <sstream>
#include <numeric>
#include <cstring>
#include <bitset>
#include <string>
#include <deque>
#include <stack>
#include <cmath>
#include <queue>
#include <set>
#include <map>
using namespace std;
#define INF 0x3f3f3f3f
#define LC(x) (x<<1)
#define RC(x) ((x<<1)+1)
#define MID(x,y) ((x+y)>>1)
#define CLR(arr,val) memset(arr,val,sizeof(arr))
#define FAST_IO ios::sync_with_stdio(false);cin.tie(0);
typedef pair<int, int> pii;
typedef long long LL;
const double PI = acos(-1.0);
const int N = 25;
int arr[N], cnt[4];
int Max_dep, Num;
char ans[1000];
int top,Back[8]={5,4,7,6,1,0,3,2};//Back数组,减掉正拉动后又马上反向拉动的无意义搜索
int pos[8][7] =
{
{1, 3, 7, 12, 16, 21, 23}, //A0
{2, 4, 9, 13, 18, 22, 24}, //B1
{11, 10, 9, 8, 7, 6, 5}, //C2
{20, 19, 18, 17, 16, 15, 14}, //D3
{24, 22, 18, 13, 9, 4, 2},//E4
{23, 21, 16, 12, 7, 3, 1},//F5
{14, 15, 16, 17, 18, 19, 20},//G6
{5, 6, 7, 8, 9, 10, 11},//H7
};
int Need(int cur[])
{
int i;
cnt[1] = cnt[2] = cnt[3] = 0;
for (i = 7; i <= 9; ++i)
++cnt[cur[i]];
for (i = 12; i <= 13; ++i)
++cnt[cur[i]];
for (i = 16; i <= 18; ++i)
++cnt[cur[i]];
int Need_1 = 8 - cnt[1], Need_2 = 8 - cnt[2], Need_3 = 8 - cnt[3];
int Min_Need = min(Need_1, min(Need_2, Need_3));
return Min_Need;
}
int IDA_star(int dep, int Arr[],int pre)
{
int Need_cur = Need(Arr);
if (Need_cur == 0)
{
Num = Arr[7];
return 1;
}
if (Need_cur + dep > Max_dep)
return 0;
int Temp_arr[N];
for (int Opsid = 0; Opsid < 8; ++Opsid)
{
if(Opsid==pre)
continue;
ans[top++] = ‘A‘ + Opsid;
for (int i = 1; i <= 24; ++i)
Temp_arr[i] = Arr[i];
for (int i = 0; i < 7; ++i)
Temp_arr[pos[Opsid][i]] = Arr[pos[Opsid][(i + 1) % 7]];
if (IDA_star(dep + 1, Temp_arr, Back[Opsid]))
return 1;
else
--top;
}
return 0;
}
int main(void)
{
while (~scanf("%d", &arr[1]) && arr[1])
{
for (int i = 2; i <= 24; ++i)
scanf("%d", &arr[i]);
if (Need(arr) == 0)
{
puts("No moves needed");
printf("%d\n", arr[7]);
}
else
{
top = 0;
Max_dep = 1;
Num = -1;
while (!IDA_star(0, arr, -1))
++Max_dep;
ans[top] = ‘\0‘;
puts(ans);
printf("%d\n", Num);
}
}
return 0;
}
POJ 2286 The Rotation Game(IDA*)
原文:http://www.cnblogs.com/Blackops/p/7008622.html