 , you can assume
, you can assume 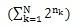 mod
N =0. Because the number is too big to count, so P mod 1000003 is instead.
mod
N =0. Because the number is too big to count, so P mod 1000003 is instead. 2 3 1 1 3 4 1 2 1 4
Case 1:4 Case 2:6
又是一条数论题目,最近学习数论,看完书本感觉并不能掌握数论的,还是需要多多练习,多运用才能掌握这个思想武器的。
本题可以简单点过,不需要太高级的数论内容;
但是也可以运用好数论的内容,可以应用上三个数论的内容:
1 扩展欧几里得
2 快速求模
3 乘法逆元(inverse of modulo)
2 快速求模,也可以生成一个数组,因为这里最大是40000,故此数值不大,可以使用数组,然后查表,速度很快。
但是这里使用快速的时间效率也几乎接近常数,没必要保存一个数组。如下面的powMod函数。
3 乘法逆元的应用的原理就是:
如果求a / b % c;
那么可以求得b的乘法逆元e;be % c == 1,那么a / b % c == a / b * b * e % c;相当于 a / b % c == a / b * 1(b*e) % c,这个是求模的性质,相当于一般算术中的一个数乘以其倒数等于1.最后可以化简为a * e % c == a / b % c;
这样做题,可以说非常科学系统,下面速度也算挺快的,而且消耗内存很小。
作者:靖心 http://blog.csdn.net/kenden23/article/details/29363389
#include <cstdio>
class DataProcessing3094
{
const static int MOD = 1000003;
long long s, t, g;
void extGCD(int a, int b)
{
if (b == 0)
{
s = 1L, t = 0L;
g = a;
}
else
{
extGCD(b, a % b);
long long tmp = s;
s = t;
t = tmp - a / b * t;
}
}
long long powMod(long long base, long long num, long long mod)
{
long long ans = 1;
while (num)
{
if (num & 1) ans = ans * base % mod;
base = base * base % mod;
num >>= 1;
}
return ans % mod;
}
public:
DataProcessing3094()
{
int T, N, a;
scanf("%d", &T);
for (int i = 1; i <= T; i++)
{
scanf("%d", &N);
long long ans = 0;
for (int j = 0; j < N; j++)
{
scanf("%d", &a);
ans = (ans + powMod(2, a, MOD)) % MOD;
}
extGCD(MOD, N);//即使g不等于1,最后mod也会约去g
t = (t % MOD + MOD) % MOD;//求其最小正整数
ans = ans * t % MOD;
printf("Case %d:%I64d\n",i,ans);
}
}
};
HDU 3049 Data Processing 数论题解,布布扣,bubuko.com
原文:http://blog.csdn.net/kenden23/article/details/29363389