Okabe likes to take walks but knows that spies from the Organization could be anywhere; that‘s why he wants to know how many different walks he can take in his city safely. Okabe‘s city can be represented as all points (x, y) such that x and y are non-negative. Okabe starts at the origin (point (0, 0)), and needs to reach the point (k, 0). If Okabe is currently at the point (x, y), in one step he can go to (x + 1, y + 1), (x + 1, y), or (x + 1, y - 1).
Additionally, there are n horizontal line segments, the i-th of which goes from x = ai to x = bi inclusive, and is at y = ci. It is guaranteed that a1 = 0, an ≤ k ≤ bn, and ai = bi - 1 for 2 ≤ i ≤ n. The i-th line segment forces Okabe to walk with y-value in the range 0 ≤ y ≤ ci when his xvalue satisfies ai ≤ x ≤ bi, or else he might be spied on. This also means he is required to be under two line segments when one segment ends and another begins.
Okabe now wants to know how many walks there are from the origin to the point (k, 0) satisfying these conditions, modulo 109 + 7.
The first line of input contains the integers n and k (1 ≤ n ≤ 100, 1 ≤ k ≤ 1018) — the number of segments and the destination xcoordinate.
The next n lines contain three space-separated integers ai, bi, and ci (0 ≤ ai < bi ≤ 1018, 0 ≤ ci ≤ 15) — the left and right ends of a segment, and its y coordinate.
It is guaranteed that a1 = 0, an ≤ k ≤ bn, and ai = bi - 1 for 2 ≤ i ≤ n.
Print the number of walks satisfying the conditions, modulo 1000000007 (109 + 7).
1 3
0 3 3
4
2 6
0 3 0
3 10 2
4
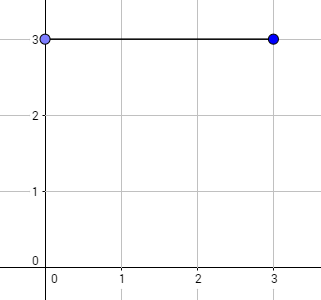
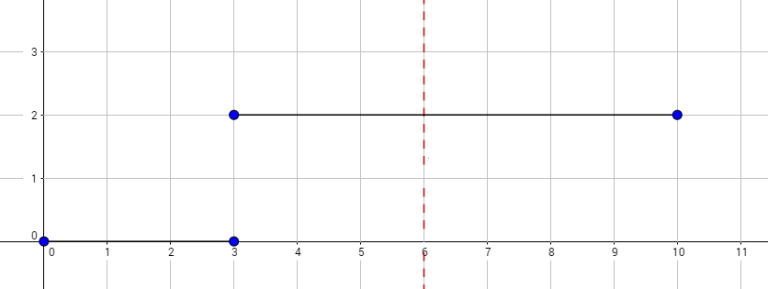
The graph above corresponds to sample 1. The possible walks are:
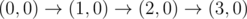
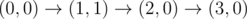
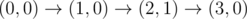
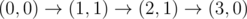
The graph above corresponds to sample 2. There is only one walk for Okabe to reach (3, 0). After this, the possible walks are:
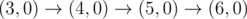
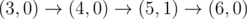
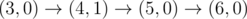
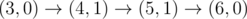
题意:给n条水平线段点终点高度,只能右上方向走,向右走,右下方向走,只能在第一象限及坐标轴上线段下面运动问到(K,0)有多少种方案
题解:可以推出DP式子,对每一条线段使用快速幂
#include <bits/stdc++.h> #define maxn 20 using namespace std; long long mod = 1e9+7, len=20, n, k, sta[110], en[110], c[110]; struct mat{ long long m[maxn][maxn];//注意初始化 mat friend operator*(mat a,mat b){ mat d; memset(d.m, 0, sizeof(d.m)); for(int i=0;i<len;i++) for(int j=0;j<len;j++) for(int k=0;k<len;k++) d.m[i][j] = (d.m[i][j]%mod+(a.m[i][k]*b.m[k][j])%mod)%mod; return d; } }; mat f(mat x,long long num){ mat t; memset(t.m, 0, sizeof(t.m)); for(int i=0;i<len;i++) t.m[i][i] = 1; while(num){ if(num&1) t = t*x; x = x*x; num >>= 1; } return t; } int main(){ int i,j; mat s, ss; memset(s.m, 0, sizeof(s.m)); memset(ss.m, 0, sizeof(ss.m)); s.m[0][0] = 1; for(i=0;i<len;i++) for(j=i-1;j<=i+1;j++) if(j>=0&&j<len) ss.m[i][j] = 1; cin>>n>>k; for(i=0;i<n;i++) cin>>sta[i]>>en[i]>>c[i]; i = 0; while(i<n&&k>=en[i]){ len = c[i]+1; s = s*f(ss, en[i]-sta[i]); i++; } len = c[i]+1; s = s*f(ss, k-en[i-1]); cout<<s.m[0][0]<<endl; return 0; }
Codeforce821E Okabe and El Psy Kongroo
原文:http://www.cnblogs.com/Noevon/p/7102777.html