Logistic回归
主要思想：
基于Logistic回归和Sigmoid函数的分类
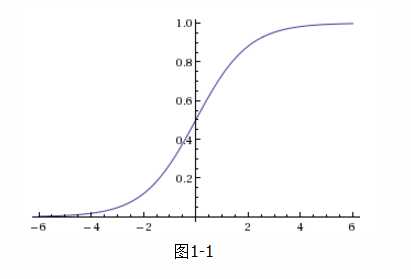
我们想要的函数应该是，能接受所有输入然后预测出类别。例如，在两个类的情况下，上述函数输出0或1。这种函数称为单位阶跃函数，该函数在跳跃点从0瞬间跳到1，这个瞬间跳跃的过程有时很难处理。所以，我们需要引用一个也具有类似性质的函数，该函数被称作Sigmoid函数，Sigmoid函数计算公式如下：
图1-1给出了Sigmoid函数的图像，当x为0的时候，Sigmoid函数值为0.5。随着x的增大，对应的Sigmoid值将逼近于1，随着x的减小，Sigmoid值将逼近于0。
我们定义向量(x1、x2……xn)是分类器的输入数据，向量θ是我们要寻找的最佳回归系数，则可以得出Sigmoid函数的输入z为：
为了方便将z作为矩阵计算，可以把x0赋值为1，将x0作为一个常亮偏移，则公式(2)则可以写成：
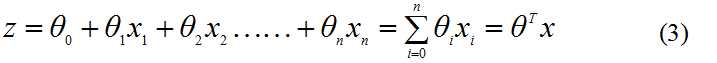
构造预测函数为：
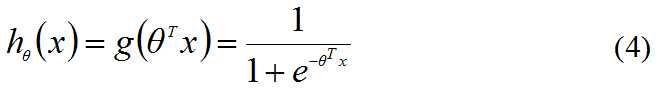
hθ(x)函数的值有特殊含义，它表示结果取1的概率，当hθ(x)大于0.5属于分类1，当hθ(x)小于0.5属于分类0。因此，对于输入x分类结果为类别1或类别0的概率分别为：
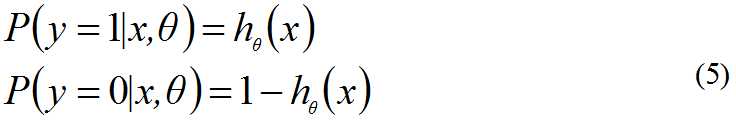
构造损失函数：
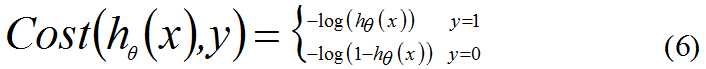
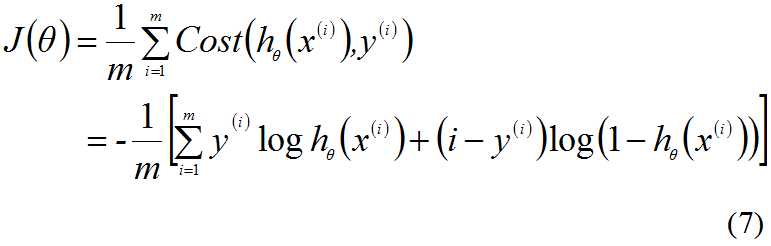
这里的Cost函数和J(θ)函数是基于最大似然估计推到得到，下面将给出推导过程。(4)式综合起来可以写成：
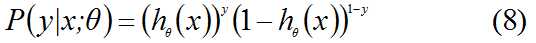
取似然函数为：
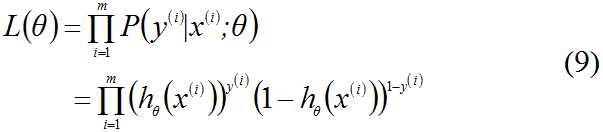
对数似然函数为：
最大似然估计就是要求得使l(θ)取最大值时的θ，这里可以用梯度上升法求解，求得θ的最佳参数，但根据(7)式和(10)式可以推出：
因为乘了一个-1/m，所以J(θ)取最小值时的θ为要求额最佳参数。
梯度上升法求J(θ)的最大值
求J(θ)的最大值可以使用梯度上升法，根据梯度上升法可得θ的更新过程：
其中，α为步长，
为梯度算子，总是指向函数值下降最快的方向，公式将一直迭代执行，直到达到某个停止条件为止，比如迭代次数达到某个指定值或算法达到某个可以允许的误差范围。
在求偏导之前，我们先对f(x)=1/(1+eg(x))函数求偏导，在之后的偏导需要用到：
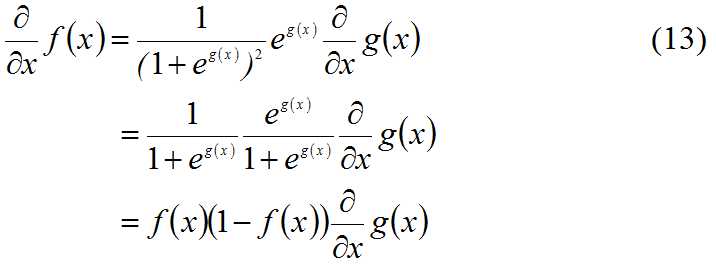
现在，对
求偏导：
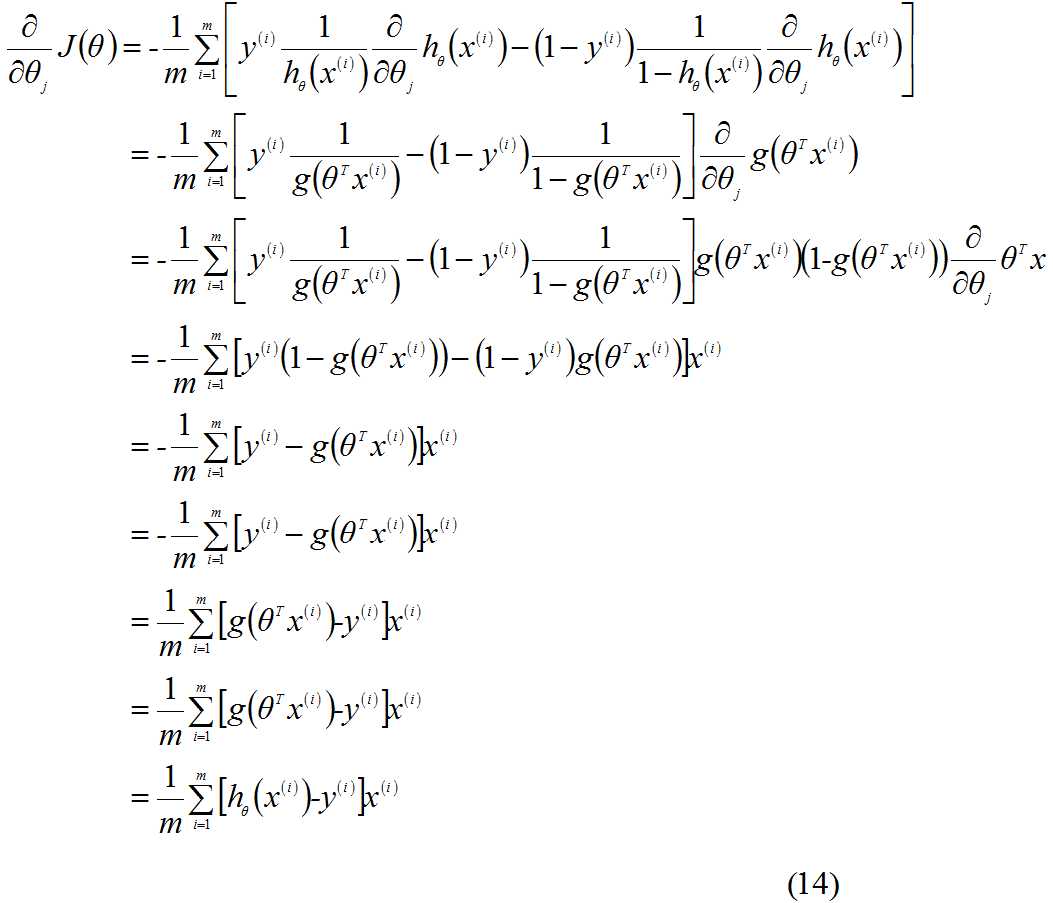
因此，(12)式的更新过程可以写成：
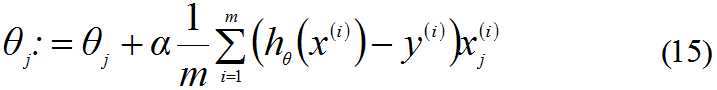
因为式中的α本来就为常量，所以1/m一般将其省略。所以，最终θ的更新过程为：
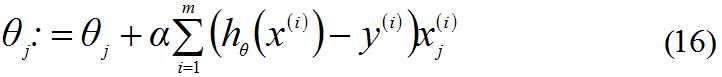
代码实现
梯度上升法的伪代码：
每个回归系数初始化为1
重复R次：
计算整个数据集的梯度
使用步长*梯度更新回归系数的向量
返回回归系数
代码1-2是Logistic回归梯度上升优化算法的实现
def loadDataSet():
dataMat = []
labelMat = []
fr = open("testSet.txt")
for line in fr.readlines():
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
labelMat.append(int(lineArr[2]))
return dataMat, labelMat
def sigmoid(inX):
return 1.0 / (1 + exp(-inX))
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn)
labelMat = mat(classLabels).transpose()
m, n = shape(dataMatrix)
alpha = 0.001
maxCycles = 500
weights = ones((n, 1))
for k in range(maxCycles):
t = dataMatrix * weights
h = sigmoid(dataMatrix * weights)
error = labelMat - h
weights += alpha * dataMatrix.transpose() * error
return weights
调用代码1-2
>>> dataArr, labelMat = loadDataSet()
>>> weights = gradAscent(dataArr, labelMat)
>>> weights
array([[ 4.12414349],
[ 0.48007329],
[-0.6168482 ]])
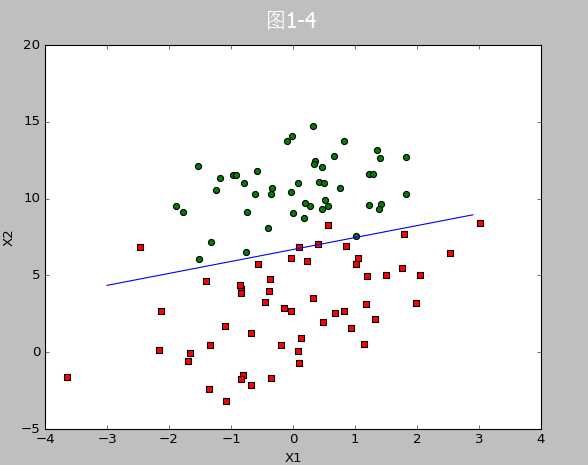
代码1-3位画出数据集与Logistic回归最佳拟合直线的函数
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat, labelMat = loadDataSet()
dataArr = array(dataMat)
n = shape(dataArr)[0]
xcord1 = [];
ycord1 = []
xcord2 = [];
ycord2 = []
for i in range(n):
if int(labelMat[i]) == 1:
xcord1.append(dataArr[i, 1]);
ycord1.append(dataArr[i, 2])
else:
xcord2.append(dataArr[i, 1]);
ycord2.append(dataArr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c=‘red‘, marker=‘s‘)
ax.scatter(xcord2, ycord2, s=30, c=‘green‘)
x = arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y)
plt.xlabel(‘X1‘);
plt.ylabel(‘X2‘);
plt.show()
调用代码1-3生成图1-4
数据集链接：http://pan.baidu.com/s/1c2MUC5E
参考文献
[1]《机器学习实战》——【美】Peter Harington
[2] https://www.coursera.org/course/ml
[3] http://blog.csdn.net/abcjennifer/article/details/7716281
[4] http://www.cnblogs.com/tornadomeet/p/3395593.html
[5] http://blog.csdn.net/jackie_zhu/article/details/8895270
[6]http://blog.csdn.net/dongtingzhizi/article/details/15962797
原文：http://www.cnblogs.com/fuxinyue/p/7096664.html