[BZOJ2154]Crash的数字表格
试题描述
输入
输出
输入示例
4 5
输出示例
122
数据规模及约定
100%的数据满足N, M ≤ 10^7。
题解
把最小公倍数转化成最大公约数,因为我们比较熟悉最大公约数。
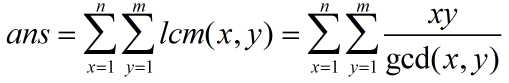
然后考虑枚举 gcd(x, y)
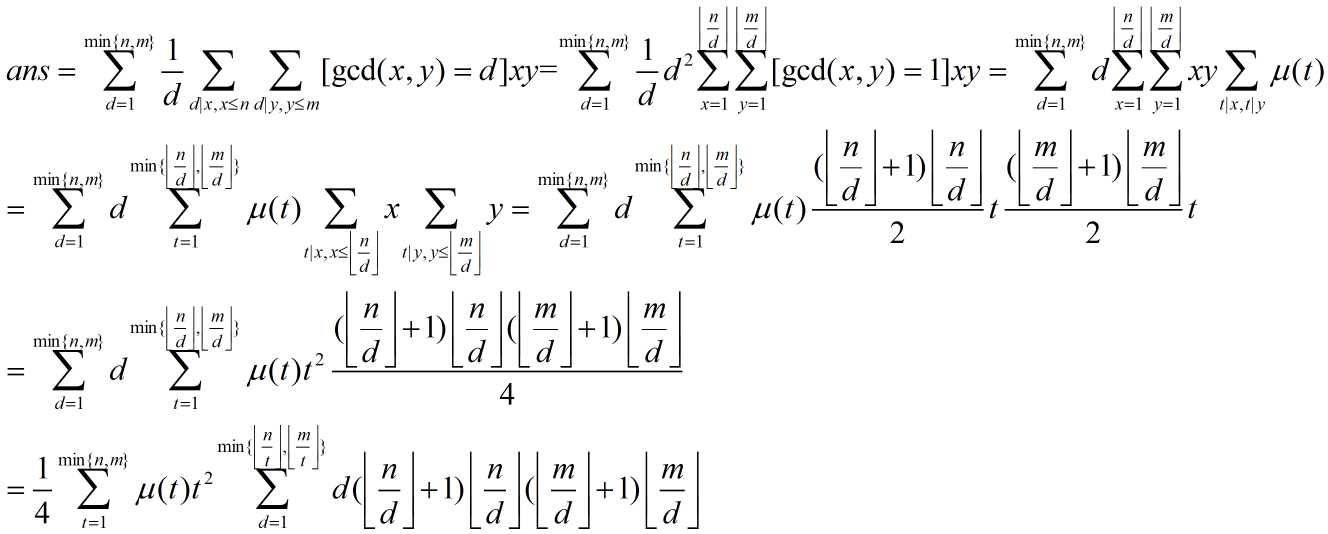
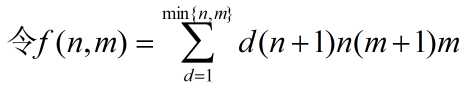
于是
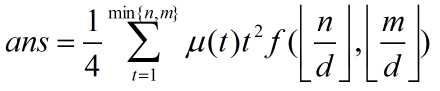
于是分两个 sqrt(n) 分别计算 f(n, m) 和 ans 就好了。
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cctype>
#include <algorithm>
using namespace std;
const int BufferSize = 1 << 16;
char buffer[BufferSize], *Head, *Tail;
inline char Getchar() {
if(Head == Tail) {
int l = fread(buffer, 1, BufferSize, stdin);
Tail = (Head = buffer) + l;
}
return *Head++;
}
int read() {
int x = 0, f = 1; char c = Getchar();
while(!isdigit(c)){ if(c == ‘-‘) f = -1; c = Getchar(); }
while(isdigit(c)){ x = x * 10 + c - ‘0‘; c = Getchar(); }
return x * f;
}
#define maxn 10000001
#define MOD 20101009
#define div4 15075757
#define LL long long
int n, m, prime[maxn], cp, mu[maxn], sum[maxn], tot[maxn];
bool vis[maxn];
void init() {
mu[1] = 1; sum[1] = 1;
for(int i = 2; i <= n; i++) {
if(!vis[i]) prime[++cp] = i, mu[i] = MOD - 1;
for(int j = 1; i * prime[j] <= n && j <= cp; j++) {
vis[i*prime[j]] = 1;
if(i % prime[j] == 0){ mu[i*prime[j]] = 0; break; }
mu[i*prime[j]] = -mu[i];
if(mu[i*prime[j]] < 0) mu[i*prime[j]] += MOD;
}
sum[i] = sum[i-1] + (LL)mu[i] * i % MOD * i % MOD;
if(sum[i] >= MOD) sum[i] -= MOD;
}
for(int i = 1; i <= n; i++) {
tot[i] = tot[i-1] + i;
if(tot[i] >= MOD) tot[i] -= MOD;
}
return ;
}
int f(int n, int m) {
int ans = 0;
for(int i = 1, lst; i <= n; i = lst + 1) {
lst = min(n / (n / i), m / (m / i));
ans += (LL)(n / i + 1) * (n / i) % MOD * (m / i + 1) % MOD * (m / i) % MOD * (tot[lst] - tot[i-1] + MOD) % MOD;
if(ans >= MOD) ans -= MOD;
}
return ans;
}
int main() {
n = read(); m = read(); int ans = 0;
if(n > m) swap(n, m);
init();
for(int i = 1, lst; i <= n; i = lst + 1) {
lst = min(n / (n / i), m / (m / i));
ans += (LL)f(n / i, m / i) * (sum[lst] - sum[i-1] + MOD) % MOD;
if(ans >= MOD) ans -= MOD;
}
printf("%lld\n", (LL)ans * div4 % MOD);
return 0;
}
原文:http://www.cnblogs.com/xiao-ju-ruo-xjr/p/7109499.html