题意 : 中文题不详述。
思路 : 黑书上116页讲的很详细。不过你需要在之前预处理一下面积,那样的话之后列式子比较方便一些。
先把均方差那个公式变形,
另X表示x的平均值,两边平方得
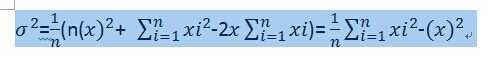 平均值是一定的,所以只要让每个矩形的总分的平方和尽量小即可。左上角坐标为(x1,y1)右下角坐标为(x2,y2)的棋盘,设总和为s[][][][],切割k次以后得到k+1块矩形的总分平方和是d[k][][][][],则可以沿着横线切也可以沿着竖线切,然后选一块接着切,递归下去,状态转移方程
平均值是一定的,所以只要让每个矩形的总分的平方和尽量小即可。左上角坐标为(x1,y1)右下角坐标为(x2,y2)的棋盘,设总和为s[][][][],切割k次以后得到k+1块矩形的总分平方和是d[k][][][][],则可以沿着横线切也可以沿着竖线切,然后选一块接着切,递归下去,状态转移方程
d[k,x1,y2,x2,y2] = min{min{d[k-1,x1,y1,a,y2]+s[a+1,y1,x2,y2],d[k-1,a+1,y1,x2,y2]+s[x1,y1,a,y2]}(x1<=a<x2),min{d[k-1,x1,y2,x2,b]+s[x1,b+1,x2,y2],d[k-1,x1,b+1,x2,y2]+s[x1,y1,x2,b]},(y1<=b<y2)}

1 //1191 2 #include <stdio.h> 3 #include <iostream> 4 #include <cmath> 5 6 using namespace std ; 7 8 double dp[15][9][9][9][9] ,s[9][9] ; 9 int n ; 10 11 double ss(int x1,int y1,int x2,int y2) 12 { 13 double sss = s[x2][y2]-s[x1-1][y2]-s[x2][y1-1]+s[x1-1][y1-1] ; 14 return sss * sss ; 15 } 16 17 double DFS(int k,int x1,int y1,int x2,int y2) 18 { 19 if(k == 1) return ss(x1,y1,x2,y2) ; 20 if(fabs(dp[k][x1][y1][x2][y2]) > 1e-6) return dp[k][x1][y1][x2][y2] ; 21 double minn = 1 << 29 ; 22 for(int i = x1 ; i < x2 ; i++) 23 minn = min(minn,min(DFS(k-1,x1,y1,i,y2)+ss(i+1,y1,x2,y2),DFS(k-1,i+1,y1,x2,y2)+ss(x1,y1,i,y2))) ; 24 for(int i = y1 ; i < y2 ; i++) 25 minn = min(minn,min(DFS(k-1,x1,y1,x2,i)+ss(x1,i+1,x2,y2),DFS(k-1,x1,i+1,x2,y2)+ss(x1,y1,x2,i))) ; 26 dp[k][x1][y1][x2][y2] = minn ; 27 return minn ; 28 } 29 int main() 30 { 31 scanf("%d",&n) ; 32 int x ; 33 //memset(s,0,sizeof(s)) ; 34 for(int i = 1 ; i <= 8 ; i++) 35 for(int j = 1 ; j <= 8 ; j++) 36 { 37 scanf("%d",&x) ; 38 s[i][j] = x + s[i-1][j]+s[i][j-1]-s[i-1][j-1] ; 39 } 40 printf("%.3lf\n",sqrt(DFS(n,1,1,8,8)/n-(s[8][8]/n)*(s[8][8]/n)) ); 41 return 0 ; 42 }
POJ 1191 棋盘分割(DP),布布扣,bubuko.com
原文:http://www.cnblogs.com/luyingfeng/p/3784271.html