一、心得
二、题目和分析
问题描述:
有一个需要使用每个资源的n个活动组成的集合S= {a1,a2,···,an },资源每次只能由一个活动使用。每个活动a都有一个开始时间和结束时间,且 0<= s < f < 。一旦被选择后,活动a就占据半开时间区间[s,f]。如果[s,f]和[s,f]互不重叠,则称两个活动是兼容的。该问题就是要找出一个由互相兼容的活动组成的最大子集。
三、代码和结果
输入
11
3 5
1 4
12 14
8 12
0 6
8 11
6 10
5 7
3 8
5 9
2 13
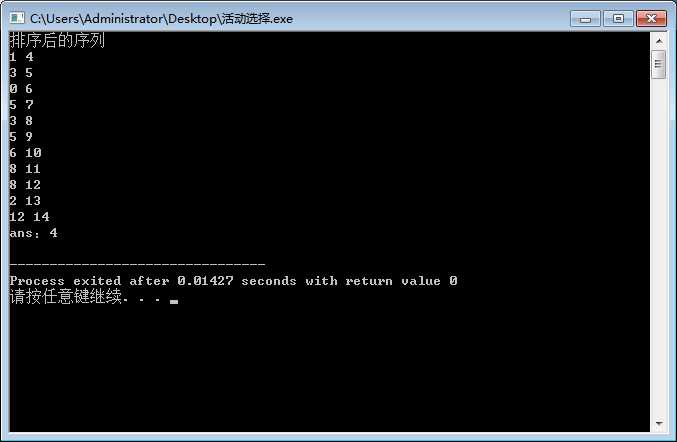
1 #include <iostream> 2 #include <algorithm> 3 using namespace std; 4 struct act{ 5 int begin; 6 int end; 7 }; 8 9 int mycmp(const act &a,const act &b){ 10 return a.end<b.end; 11 } 12 13 //贪心,选最快结束就好 14 int main(){ 15 freopen("in.txt","r",stdin); 16 int n; 17 cin>>n; 18 act a[1005]; 19 for(int i=1;i<=n;i++){ 20 cin>>a[i].begin>>a[i].end; 21 } 22 sort(a+1,a+n+1,mycmp); 23 cout<<"排序后的序列"<<endl; 24 for(int i=1;i<=n;i++){ 25 cout<<a[i].begin<<" "<<a[i].end<<endl; 26 } 27 int total=0; 28 int begin=0; 29 for(int i=1;i<=n;i++){ 30 if(a[i].begin>=begin){ 31 total++; 32 begin=a[i].end; 33 } 34 35 } 36 cout<<"ans:"<<total<<endl; 37 38 return 0; 39 }
原文:http://www.cnblogs.com/Renyi-Fan/p/7135613.html