1.通常对只有一个key的记录来排序时,若两个记录的key相同,稳定排序不会改变排序前
后的顺序。
2.对有多个key来说,如基数排序,从次要key开始排序,在次要key排序完成后,a1排在
a2前,而a1和a2优先级大的key相同,当优先级大的key排序完成后a1会仍在a2前,保
持了稳定性。
1.用于多个key的排序,如基数排序这样。
2.用于单个key的排序,如果key相同就不要改变它们的次序:
比如你要给一个结构体排序,要求按a的大小排序,a相同的话,按输入顺序输出。
a=4 b=100,a=1,b=200,a=4,b=300,a=5,b=400
你如果冒泡的话(所有的稳定排序都行),会输出
a=1 b=200,a=4 b=100,a=4 b=300,a=5 b=400
但如果快排的话很可能输出
a=1 b=200,a=4 b=300,a=4 b=100,a=5 b=400
在解决某些问题时,你会发再用不稳定排序是做不到的。
#include <iostream.h> void InsertSort(int seq[],int len){ int tem; //辅助空间tem,o(1) for(int i=1;i<len;i++) //从第二个开始找 if(seq[i]<seq[i-1]){ //如果小于前一个 tem = seq[i]; //提取出来 seq[i] = seq[i-1]; //先后移一格 for(int j=i-2;j>=0&&tem<seq[j];j--)//从前两个开始往前找,直到大于等于时停止 seq[j+1] = seq[j]; //边找边后移 seq[j+1] = tem; //放入正确位置 } } void main() { int len = 8; int seq_test[] = {5,9,8,10,30,1,45,34}; InsertSort(seq_test,len); for(int i=0;i<len;i++) cout<<seq_test[i]<<endl; }
//shell就是用的直接插入思路,只是多加一个增量dk,dk=1时就是直接插入排序(基本有序思想) void ShellSort(int seq[],int len,int dk){ int tem; for(int i=dk;i<len;i++) if(seq[i]<seq[i-dk]){ tem = seq[i]; seq[i] = seq[i-dk]; for(int j=i-2*dk;j>=0&&tem<seq[j];j-=dk) seq[j+dk] = seq[j]; seq[j+dk] = tem; } }
void SelectSort(int seq[],int len){ int tem,k; //K为最小值的下标 for(int i=0;i<len-1;i++){ //总共进行len-1次排序 k = i; for(int j=i+1;j<len;j++) if(seq[j]<seq[k]) k = j; if(k!=i){ tem = seq[i]; seq[i] = seq[k]; seq[k] = tem; } } }
void HeapAdjust(int seq[],int left,int right){ //左边界,右边界 int head; head = seq[left]; //要排序的头结点 for(int i=left*2;i<=right;i*=2){ //i当作上指针,left当作下指针 if(i<right&&seq[i]<seq[i+1]) i++; if(head>=seq[i]) break; seq[left] = seq[i]; left = i; } seq[left] = head; } void HeapSort(int seq[],int len){ int tem,i; for(i=len/2;i>0;i--) //将无序二叉树调整为大顶堆 HeapAdjust(seq,i,len); for(i=len;i>1;i--){ //边排列边调整 tem = seq[1]; seq[1] = seq[i]; seq[i] = tem; HeapAdjust(seq,1,i-1); } }
void BubbleSort(int seq[],int len){ int tem; for(int i=0;i<len-1;i++) //排序要走的趟次,满足len-1趟即可 for(int j=0;j<len-1-i;j++)//排序范围,起始0~len-1,且每次减1 if(seq[j]>seq[j+1]){ tem = seq[j]; seq[j] = seq[j+1]; seq[j+1] = tem; } } 也计你会问:为什么冒泡排序最好情况下时间复杂度为o(n)?因为还可以这样来改进: void BubbleSort2(int seq[],int len){ int tem; int FLAG; //增加一位标志 for(int i=0;i<len-1;i++){ FLAG = 0; //每趟初始为0 for(int j=0;j<len-1-i;j++) if(seq[j]>seq[j+1]){ tem = seq[j]; seq[j] = seq[j+1]; seq[j+1] = tem; FLAG = 1; //交换过说明序列无序,置为1 } if(!FLAG) //为0说明已经排序完成,直接返回 return; } }
int Partition(int seq[],int low,int high){ //一次划分排序 int pivotkey = seq[low]; //取最低位为轴点 while(low<high){ //循环直到low high相遇 while(low<high&&seq[high]>=pivotkey) high--; //首先从最高点开始找 seq[low] = seq[high]; while(low<high&&seq[low]<=pivotkey) low++; seq[high] = seq[low]; } seq[low] = pivotkey; //最终位置,此时low=high return low; //返回划分界点 } void QuickSort(int seq[],int low,int high){ //递归直到low=high时结束排序 int pivotloc; //划分界点位置 if(low<high){ pivotloc = Partition(seq,low,high); QuickSort(seq,low,pivotloc-1); QuickSort(seq,pivotloc+1,high); } }
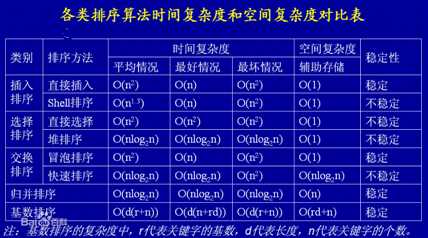
快排:最常用的排序算法,速度通常也是最快的。
时间复杂度:O(n*logn)
最坏:O(n^2)
空间复杂度:O(n*logn)
不稳定
堆排:特别适用于数据量很大的场合(百万级数据)。因为快排和归并排序都是基于递归的,数据量很大的情况下容易发生堆栈溢出。
时间复杂度:O(n*logn)好、坏、平均一样
空间复杂度:O (1)
排序速度略低于快排。
不稳定
归并排序:稳定
时间复杂度:O(n*logn)好、坏、平均一样
空间复杂度:O(n)
值得注意的是,它是一种稳定的排序算法。
与前两种排序算法不同的是,归并排序需要额外的数组开销。
原文:http://www.cnblogs.com/mzzcy/p/7142421.html