③ 将00100111左移两位的结果是10011100,数值变成了原来的4倍,用十进制表示的话,数值从39变成了156,也正好是4倍。这与十进制的移位运算也是符合的,十进制数左移后也会变成原来的10倍、100倍。1000倍……同样,二进制数左移后也会变成原来的2倍、4倍、8倍,反之右移就会变成原来的1/2、1/4、1/8。
上一小节说了,右移的操作说明会在后续说明,这里就是后续了。先补充一个知识点:计算机在做减法运算时,实际上内部是在做加法运算的。
右移后空出来的高位数值,有0和1两种形式,要想区分什么时候补0什么时候补1,只要掌握了用二进制数表示负数的方法就可以了。
二进制数中表示负数值时,一般会把最高位作为符号来使用,因此我们把这个最高位成为符号位。符号位为0表示正数,1表示负数。那么-1用8位二进制数怎么表示呢,很多人会认为是10000001,其实这是错的,二进制表示为11111111。计算机是用“二进制的补数”来表示负数的。补数就是用整数来表示负数,过程就是:取反+1。所谓取反,就是将各数位的0反转成1,1取反为0。大家现在就可以试试-1的8进制表示形式了。
补数的思考方式虽然直观上不易理解,但逻辑上却非常严谨,大家可以试试1-1的运算,也就是1+(-1)运算。

上图的运算很明显是错的,这时,我们把-1表示成11111111来进行运算。
为什么使用补数后就能正确地表示负数了呢?大家可以再详细的看看上图,有一个位溢出去了,而溢出的那一位数计算机是不进行处理的。
有一个法则大家必须牢记:"将二进制数的值取反后加1的结果,和原来的值相加,结果为0”这个法则。
总之,要想结果为0,就必须通过补数来实现。当然,结果不为0的运算同样可以通过使用补数来得到正确的结果,不过,有一点需要注意,当运算结果为负数时,计算结果的值也是以补数的形式来表示的。
3-5的运算:
3:00000011
-5:11111011
00000011+11111011=11111110,最高位变成了1。这就代表结果为一个负数。那11111110表示的负数是多少呢?负负得正大家都知道,所以通过求解补数的补数,就可知道该值的绝对值。所以11111110,取反后加1后为00000010,十进制就是2。所以结果就是-2。
编程语言包含的整数数据类型中,有的可以表示负数,有的也不能表示。C语言中的unsigned short类型,能表示的范围就是0~65535。而short类型是-32768~32767.
大家可以仔细思考一下-32768~32767这样负数比正数多一个的原因。(+0和-0)
5、逻辑右移和算术右移的区别
开始区分右移高位的区分:
① 当二进制数的值表示图形模式而非数值时,移位后需要在最高位补0、类似于霓虹灯往右滚动的效果,这就成为逻辑右移。
② 将二进制数作为带符号的数值进行运算时,移位后要在最高位填充移位前符号位的值(0或1)。这就是算术右移。如果数值是用补数表示的负数值,那么右移后在空出来的最高位补1,就可以正确地实现1/2、1/4等的运算。如果是正数,就补0。
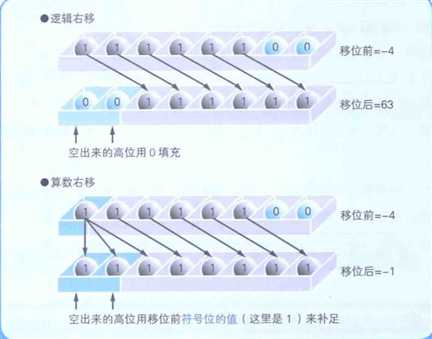
③ 只有在右移时才必须区分逻辑位移和算术位移。左移时,无论是图形模式(逻辑左移)还是相乘运算(算术左移),都只需要在空出来的低位补0即可。
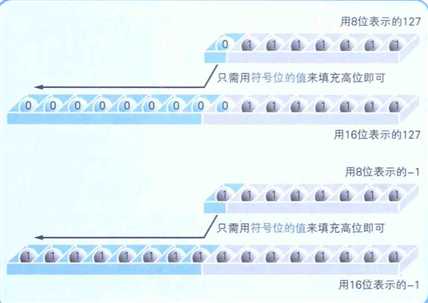
④ 符号扩充:就是指在保持值不变的前提下将其转换成16位和32位的二进制数。那怎么扩充呢,很简单,不管是正数还是用补数表示的负数,都只需用符号位的值(0或者1)填充高位即可。
6、掌握逻辑运算的窍门
计算机能处理的运算,大体可分为算术运算与逻辑运算。算术运算是指加减乘除四则运算。逻辑运算是指对二进制数各数字位的0和1分别进行处理的运算,包括逻辑非(NOT运算)、逻辑与(AND运算)、逻辑或(OR运算)和逻辑异或(XOR运算)四种。
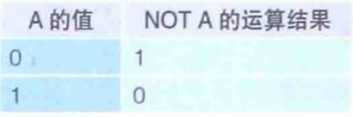
① 逻辑非指的是0变成1、1变成0的取反操作。
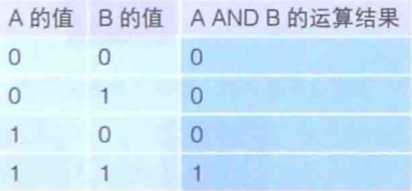
② 逻辑与指的是“两个都是1”时,运算结果才为1,其他情况下运算结果都为0的运算;
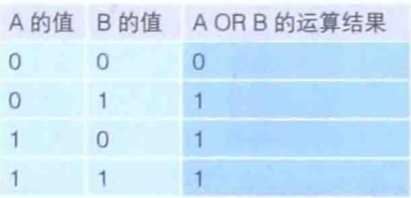
③ 逻辑或指的是“至少有一方是1”时,运算结果为1,其他情况下运算结果都是0的运算;
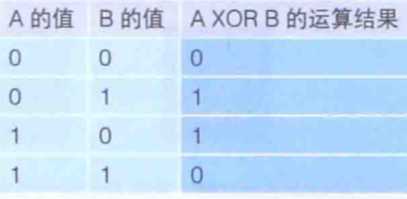
④ 逻辑异或指的是排斥相同数值的运算,“两个数值不同”,也就是说,当“其中一方是1,另一方是0”时运算结果是11,其他情况下结果都是0
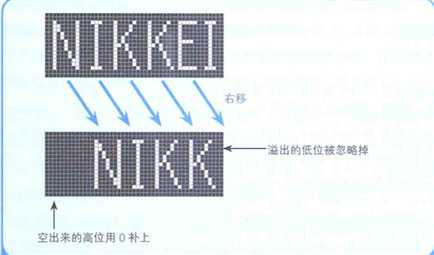
下图是对NIKKEI的头两个字母NI这一图形模式进行各种逻辑运算后的结果。假定白色部分表示1,黑色部分表示0。





.png)
.png)
.png)

.png)