2014.06.15 22:14
简介:
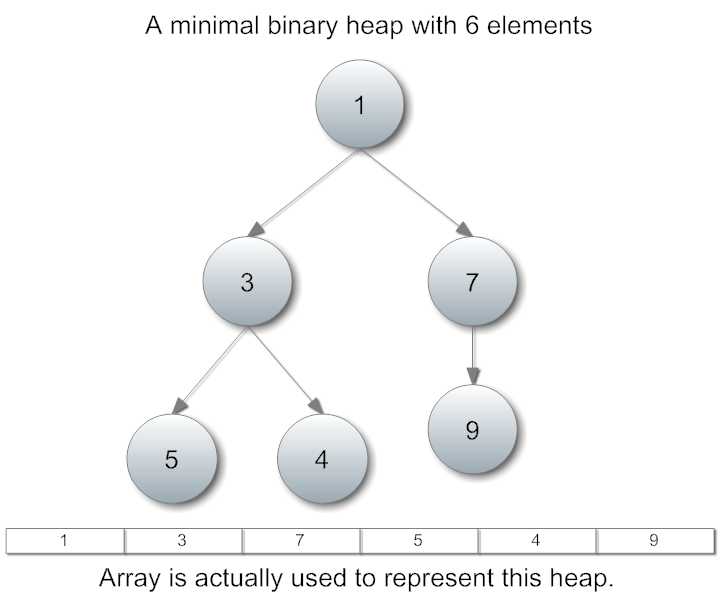
堆是一种非常实用的数据结构,其中以二叉堆最为常用。二叉堆可以看作一棵完全二叉树,每个节点的键值都大于(小于)其子节点,但左右孩子之间不需要有序。我们关心的通常只有堆顶的元素,而整个堆则被封装起来,保存在一个数组中。
图示:
下图是一个最大堆:
实现:
优先队列是STL中最常用的工具之一,许多算法的优化都要利用堆,使用的工具就是优先队列。STL中的优先队列通过仿函数来定义比较算法,此处我偷懒用了“<”运算符。关于使用仿函数的好处,我之后如果有时间深入学习STL的话,再写博文分析吧。
1 // My implementation for priority queue using binary heap. 2 #include <iostream> 3 #include <string> 4 #include <vector> 5 using namespace std; 6 7 template <class T> 8 class PriorityQueue { 9 public: 10 PriorityQueue() { 11 m_data.push_back(0); 12 } 13 14 PriorityQueue(const vector<T> &data) { 15 m_data.push_back(0); 16 for (size_t i = 0; i < data.size(); ++i) { 17 m_data.push_back(data[i]); 18 } 19 _makeHeap(); 20 } 21 22 bool empty() { 23 return m_data.size() == 1; 24 } 25 26 size_t size() { 27 return m_data.size() - 1; 28 } 29 30 T top() { 31 return m_data[1]; 32 } 33 34 void push(const T &val) { 35 m_data.push_back(val); 36 37 int n = size(); 38 int i = n; 39 40 while (i > 1) { 41 if (m_data[i / 2] < m_data[i]) { 42 _swap(m_data[i / 2], m_data[i]); 43 i /= 2; 44 } else { 45 break; 46 } 47 } 48 } 49 50 void pop() { 51 int n = size(); 52 m_data[1] = m_data[n]; 53 m_data.pop_back(); 54 --n; 55 56 int i = 1; 57 T max_val; 58 while (i * 2 <= n) { 59 max_val = i * 2 == n ? m_data[i * 2] : _max(m_data[i * 2], m_data[i * 2 + 1]); 60 if (m_data[i] < max_val) { 61 if (max_val == m_data[i * 2] || i * 2 == n) { 62 _swap(m_data[i], m_data[i * 2]); 63 i = i * 2; 64 } else { 65 _swap(m_data[i], m_data[i * 2 + 1]); 66 i = i * 2 + 1; 67 } 68 } else { 69 break; 70 } 71 } 72 } 73 74 void clear() { 75 m_data.resize(1); 76 } 77 78 ~PriorityQueue() { 79 m_data.clear(); 80 } 81 private: 82 vector<T> m_data; 83 84 T _max(const T &x, const T &y) { 85 return x > y ? x : y; 86 } 87 88 void _swap(T &x, T &y) { 89 T tmp; 90 91 tmp = x; 92 x = y; 93 y = tmp; 94 } 95 96 void _makeHeap() { 97 int n = size(); 98 int i, j; 99 T max_val; 100 101 for (j = n / 2; j >= 1; --j) { 102 i = j; 103 while (i * 2 <= n) { 104 max_val = i * 2 == n ? m_data[i * 2] : _max(m_data[i * 2], m_data[i * 2 + 1]); 105 if (m_data[i] < max_val) { 106 if (max_val == m_data[i * 2] || i * 2 == n) { 107 _swap(m_data[i], m_data[i * 2]); 108 i = i * 2; 109 } else { 110 _swap(m_data[i], m_data[i * 2 + 1]); 111 i = i * 2 + 1; 112 } 113 } else { 114 break; 115 } 116 } 117 } 118 119 n = size(); 120 cout << ‘[‘; 121 for (int i = 1; i <= n; ++i) { 122 cout << m_data[i] << ‘ ‘; 123 } 124 cout << ‘]‘ << endl; 125 } 126 }; 127 128 int main() 129 { 130 vector<int> v; 131 v.push_back(1); 132 v.push_back(2); 133 v.push_back(3); 134 v.push_back(4); 135 v.push_back(5); 136 v.push_back(6); 137 v.push_back(7); 138 v.push_back(8); 139 PriorityQueue<int> pq(v); 140 string s; 141 int n; 142 143 while (cin >> s) { 144 if (s == "push") { 145 cin >> n; 146 pq.push(n); 147 } else if (s == "pop") { 148 pq.pop(); 149 } else if (s == "top") { 150 cout << pq.top() << endl; 151 } else if (s == "end") { 152 while (!pq.empty()) { 153 pq.pop(); 154 } 155 break; 156 } 157 } 158 159 return 0; 160 }
《数据结构与算法分析:C语言描述》复习——第五章“堆”——二叉堆,布布扣,bubuko.com
《数据结构与算法分析:C语言描述》复习——第五章“堆”——二叉堆
原文:http://www.cnblogs.com/zhuli19901106/p/3790119.html