LDA是一个关于语料的生成概率模型,基本思想是文档可以表达为隐含主题的随机混合,每个主题刻画为关于词语的分布。
LDA假设在语料D中生成一篇文章w的过程如下:
1.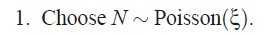 根据泊松分布选在文章长度N
根据泊松分布选在文章长度N
2. 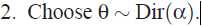 选择主题分布
选择主题分布
3. 对于每一个词Wn
(a) 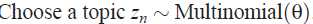 根据多项式分布选择一个主题
根据多项式分布选择一个主题
(b) 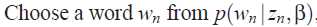 根据多项式条件概率分布选择Wn
根据多项式条件概率分布选择Wn
一些基本模型的简单假设:
(1)主题个数k是预先设定的;
(2)主题和词的概率分布矩阵式一个k*V的矩阵,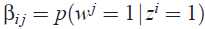
(3)文章长度N与其它变量独立
K维的Dirichlet随机变量θ服从以下概率分布
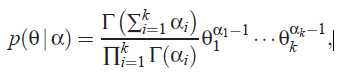
给定参数α和β,关于主题混合θ,N个主题z,N个词语w的联合概率分布如下:
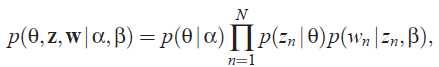
对θ进行积分,对z进行加和得到关于文档的边缘概率分布:
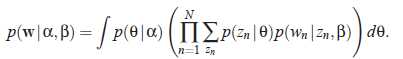
对单个文档的边缘概率分布进行加和,我们得到关于语料的概率分布:
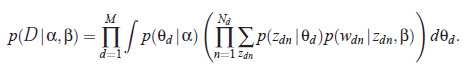
LDA的图模型的表达如下:
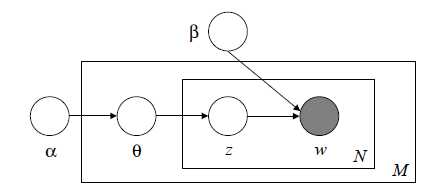
其中α和β是语料级别的参数,θd 是文档级别参数,对于每一篇文档,该参数不同,Zdn和Wdn是词语级别的参数。
一元连续混合
关于文档的概率分布
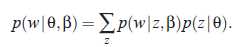
本方法与上面比较少了一个步骤,直接通过θ得到词的概率分布,中间不用选择主题z
四、与其它隐变量模型之间的关系
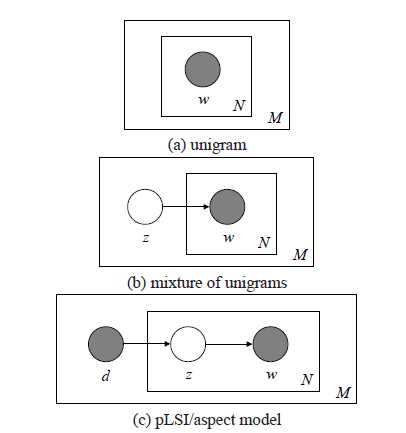
1. 一元模型
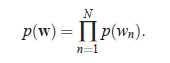 ,在没有主题的情况下,只看词语的联合分布
,在没有主题的情况下,只看词语的联合分布
2. 混合一元模型
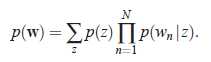 文章中所c有的词语只对应一个主题,即所有的词语都是有同一个主题生成的
文章中所c有的词语只对应一个主题,即所有的词语都是有同一个主题生成的
3. pLSI(probabilistic latent semantic indexing 潜在意义索引)概率模型
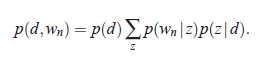 ,每篇文章可以有多个主题,
,每篇文章可以有多个主题,
但是
a. 概率模型职能用于训练数据,不能用户未来输入的数据
b. 参数个数随着文章个数呈线性增长
c. 每个文档对应的主题分布是相同的
五、推断和参数估计
1. 推断
推断的关键问题是给定文章计算隐含变量的后验分布
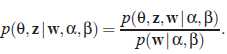
其中: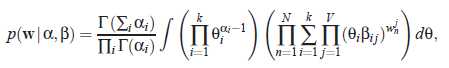
2. 变分法推断
上面提到的推断算法是很难实现的,可以在原LDA贝叶斯网络上删除部分边和节点得到以下推断图
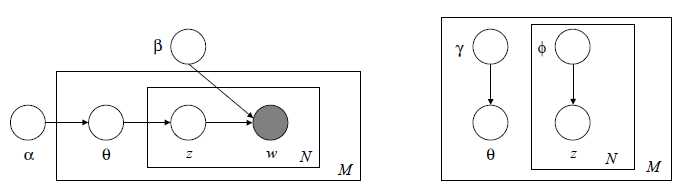
该图将θ 和z的依赖独立开来,并且删除w, 可以用以下概率分布描述
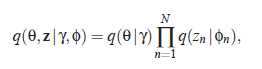
根据指定的简化版概率分布,通过最小化交叉熵KL计算γ和Φ来近似θ 和z
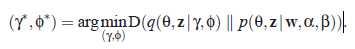
得到以下近似求解
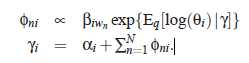
而θ 的数学期望如下:
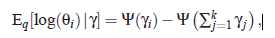
变量推断算法如下:
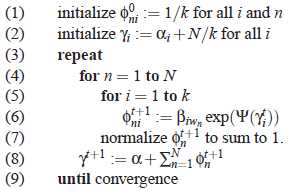
通过该算法求出γ和Φ
3. 参数估计
给定语料库D求参数α和β的最大似然估计
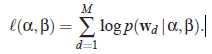
然而直接计算上面似然函数比较困难,但是上面讲到的变量推断算法为我们提供了便利的方法。
下面用EM算法进行迭代求解
A. E-step:对于每篇文档求变量参数的优化值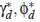 ,步骤如上
,步骤如上
B. M-step: 对α和β求最大似然估计
两个步骤迭代进行,直到收敛
4. 平滑
最好的办法就是应用变量推断的方法进行平滑。其中β是一个k*V的矩阵,每一行都可以看做一个可交换的dirichlet分布,该分布的参数为标量η。
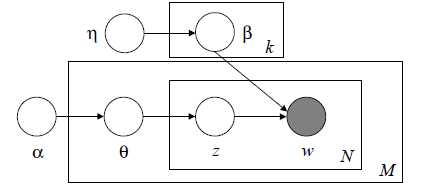
这里的η本质上就是一个先验数据,可以看做一个正则化项
Latent Dirichlet allocation学习笔记,布布扣,bubuko.com
Latent Dirichlet allocation学习笔记
原文:http://www.cnblogs.com/fanzhijun/p/3775719.html