https://flystarhe.github.io/2016/07/13/hmm-memm-crf/参考:
http://blog.echen.me/2012/01/03/introduction-to-conditional-random-fields/
标记偏置问题:MEMM最大熵马尔可夫模型
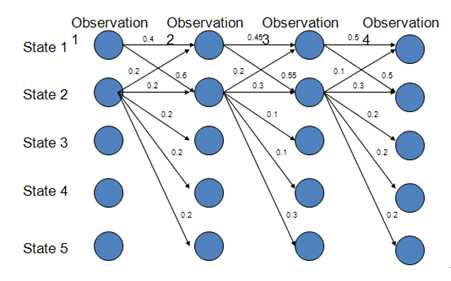
路径1-1-1-1的概率:0.4*0.45*0.5=0.09
路径2-2-2-2的概率:0.2*0.3*0.3=0.018
路径1-2-1-2的概率:0.6*0.2*0.5=0.06
存在的问题:State 1中每个结点都倾向于转移到State 2,由于MEMM的局部归一化特性,使得转出概率的分布不均衡,最终导致状态的转移存在不公平的情况
如果把每个节点转出概率和为1的限制去掉,比如我们简单把图中State 2中每个结点出发的边的概率值×10
路径1-1-1-1的概率:0.4*0.45*0.5=0.09
路径2-2-2-2的概率:2*3*3=18
路径1-2-1-2的概率:0.6*2*0.5=0.6
HMM,MEMM,CRF
HMM模型中两个假设:一是输出观察值之间严格独立,二是状态的转移过程中当前状态只与前一状态有关(一阶马尔可夫模型)
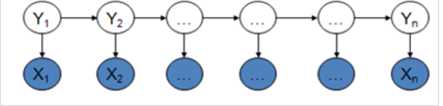
MEMM模型克服了观察值之间严格独立产生的问题
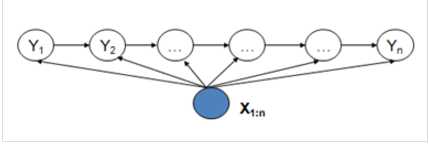
CRF模型解决了标注偏置问题
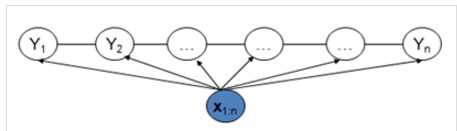
对分数进行标准化和归一化:
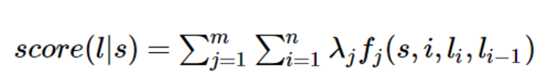
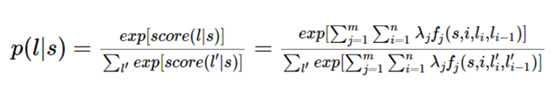
CRF的求解
优化采用的是带惩罚项的极大似然估计
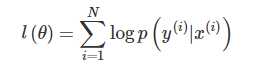
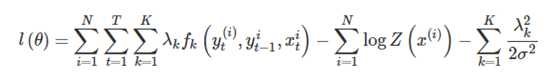
求解可以用梯度上升,牛顿法,BFGS
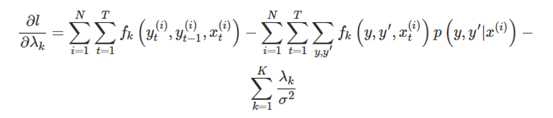
HMM的定义:(每个HMM都能对应莫个CRF)
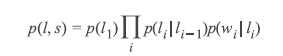

CRF可以定义数量更多,种类更丰富的特征函数。HMM模型具有天然具有局部性,就是说,在HMM模型中,当前的单词只依赖于当前的标签,当前的标签只依赖于前一个标签。这样的局部性限制了HMM只能定义相应类型的特征函数,我们在上面也看到了。但是CRF却可以着眼于整个句子s定义更具有全局性的特征函数,如这个特征函数:
CRF可以使用任意的权重 将对数HMM模型看做CRF时,特征函数的权重由于是log形式的概率,所以都是小于等于0的,而且概率还要满足相应的限制
原文:http://www.cnblogs.com/wuxiangli/p/7196984.html