首先我们要试验的是 人体脂肪fat和年龄age以及体重weight之间的关系,我们的目标就是得到一个最优化的平面来表示三者之间的关系:
TensorFlow的程序如下:
import tensorflow as tf import numpy as np import matplotlib.pyplot as plt W = tf.Variable(tf.zeros([2, 1], name="weight_age")) b = tf.Variable(0.0, name="bias") def inference(X): return tf.matmul(X, W) + b def loss(X, Y): Y_predicted = inference(X) return tf.reduce_sum(tf.square(Y-Y_predicted)) def inputs(): weight_age = [[84,46],[93,20],[65,52],[70,30],[76,57],[69,25],[63,28],[72,36],[79,57],[75,44] ,[27,24],[89,31],[65,52],[57,23],[59,60],[69,48],[60,34],[79,51],[75,50],[82,34] ,[59,46],[67,23],[85,37],[55,40],[63,30]] blood_fat_content = [354,190,405,263,451,302,288,385,402,365,209,290,346 ,254,395,434,220,374,308,220,311,181,274,303,244] return tf.to_float(weight_age), tf.to_float(blood_fat_content) def train(total_loss): learning_rate = 0.00000001 return tf.train.GradientDescentOptimizer(learning_rate).minimize(total_loss) def evaluate(sess, X, Y): print sess.run(inference([[80., 25.]])) print sess.run(inference([[65., 25.]])) init = tf.global_variables_initializer() with tf.Session() as sess: sess.run(init) X, Y = inputs() total_loss = loss(X, Y) print "The total_loss:",total_loss train_op = train(total_loss) training_steps = 10000 for step in range(training_steps): sess.run([train_op]) if step % 1000 == 0: print "loss:", sess.run([total_loss]) evaluate(sess, X, Y)
print ‘W is:‘,W.eval()
print ‘b is:‘,b.eval() sess.close()
程序中的数据散点图如下:
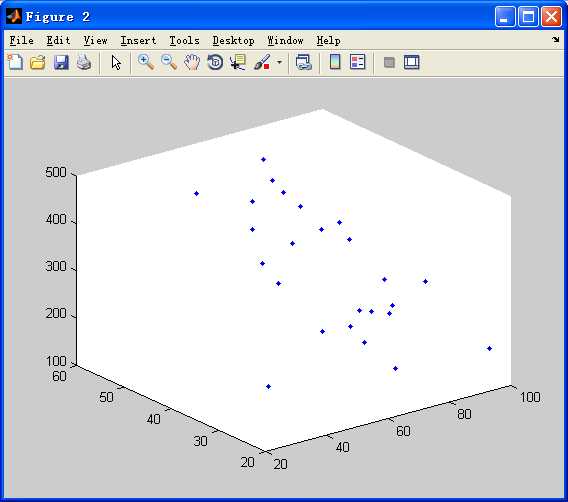
通过TensorFlow得到的最终的W的取值和b的取值如下所示:
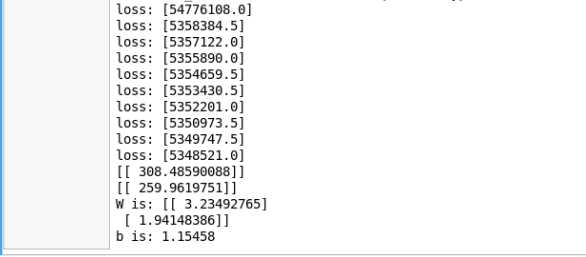
现在我们将得到的W的数据和b的数据绘制平面(MATLAB程序如下):
% TensorFlow Data Plot Script For Matlab% weight_age = [[84,46];[93,20];[65,52];[70,30];[76,57];[69,25];[63,28];[72,36]; [79,57];[75,44];[27,24];[89,31];[65,52];[57,23];[59,60];[69,48];[60,34]; [79,51];[75,50];[82,34];[59,46];[67,23];[85,37];[55,40];[63,30]]; % 25*2 weight = weight_age(:,1); %25*1 age = weight_age(:,2); %25*1 blood_fat_content = [354,190,405,263,451,302,288,385,402,365,209,290,346,254,395,434,220,374,308,220,311,181,274,303,244]; % 1*25 Fat = zeros(max(weight),max(age)); for i=1:25 Fat(weight(i),age(i)) = blood_fat_content(i); end figure,plot3(weight,age,blood_fat_content‘,‘.‘) hold on % 平面拟合 A = 3.23492765; B = 1.94148386; C = 1.15458; [x,y] = meshgrid(0:1:90); z = A*x+B*y+C; mesh(z)
结果图如下所示:
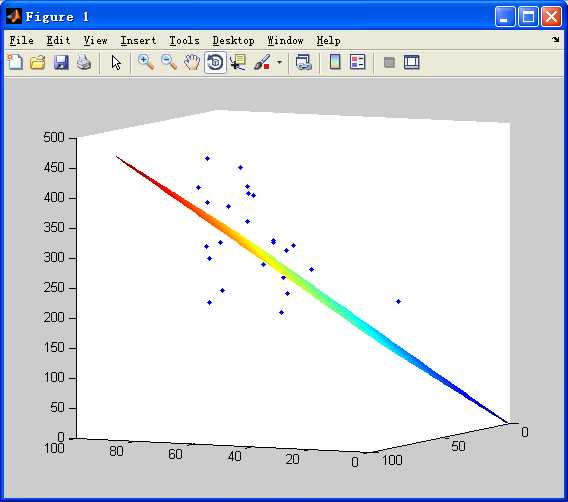
注:这里在实验的过程中,碰到一些问题,当我把learning_rate设置为0.000001时,未能得到相应的结果,total_loss=nan,也就是说梯度下降法的过程没有收敛,导致无法得到相应的数据结果!(还需要注意你的是python3还是Python2,这里的print 需要修改一下哦!)关于参数设定的学习还是慢慢来吧~
原文:http://www.cnblogs.com/uestc-mm/p/7197995.html