十大基础实用算法之快速排序和堆排序

QUICK_SORT(A,p,r)
    if(p<r)
        thenq<——PARTITION(A,p,r)
            QUICK_SORT(A,p,q-1)
            QUICK_SORT(A,q+1,r)
 
//核心函数，对数组A[p,r]进行就地重排，将小于A[r]的数移到数组前半部分，将大于A[r]的数移到数组后半部分。
//
PARTITION(A,p,r)
    pivot<——A[r]
    i<——p-1
    forj<——ptor-1
        doifA[j]<pivot
            i<——i+1
            exchangeA[i]<——>A[j]
    exchangeA[i+1]<——>A[r]
returni+1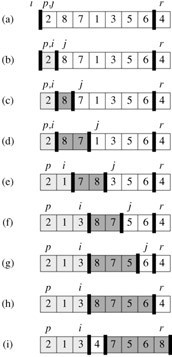

一个快速排序的实现代码如下

<span style="font-size:18px;">#include <stdio.h>
intpartition(int*arr,intlow,inthigh)
{
    intpivot=arr[high];
    inti=low-1;
    intj,tmp;
    for(j=low;j<high;++j)
        if(arr[j]<pivot){
            tmp=arr[++i];
            arr[i]=arr[j];
            arr[j]=tmp;
        }
    tmp=arr[i+1];
    arr[i+1]=arr[high];
    arr[high]=tmp;
    returni+1;
}
voidquick_sort(int*arr,intlow,inthigh)
{
    if(low<high){
        intmid=partition(arr,low,high);
        quick_sort(arr,low,mid-1);
        quick_sort(arr,mid+1,high);
    }
}
//test
intmain()
{
    intarr[10]={1,4,6,2,5,8,7,6,9,12};
    quick_sort(arr,0,9);
    inti;
    for(i=0;i<10;++i)
        printf("%d ",arr[i]);
}</span>

算法复杂度

最坏情况下的快排时间复杂度：

最坏情况发生在划分过程产生的俩个区域分别包含n-1个元素和一个0元素的时候，
即假设算法每一次递归调用过程中都出现了，这种划分不对称。那么划分的代价为O（n），
因为对一个大小为0的数组递归调用后，返回T（0）=O（1）。
估算法的运行时间可以递归的表示为：

T（n）=T（n-1）+T（0）+O（n)=T(n-1)+O(n).
可以证明为T（n）=O（n^2）。

因此，如果在算法的每一层递归上，划分都是最大程度不对称的，那么算法的运行时间就是O（n^2）。
最快情况下快排时间复杂度：

最快情况下，即PARTITION可能做的最平衡的划分中，得到的每个子问题都不能大于n/2.
因为其中一个子问题的大小为|_n/2_|。另一个子问题的大小为|-n/2-|-1.
在这种情况下，快速排序的速度要快得多：
T(n)<=2T（n/2）+O（n）.可以证得，T（n）=O（nlgn）。

堆排序算法

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

堆排序的平均时间复杂度为Ο(nlogn) 。

算法步骤：

1. 创建一个堆H[0..n-1]
2. 把堆首（最大值）和堆尾互换

3. 把堆的尺寸缩小1，并调用shift_down(0),目的是把新的数组顶端数据调整到相应位置

4. 重复步骤2，直到堆的尺寸为1

1.堆

堆实际上是一棵完全二叉树，其任何一非叶节点满足性质： Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]或者Key[i]>=Key[2i+1]&&key>=key[2i+2] 即任何一非叶节点的关键字不大于或者不小于其左右孩子节点的关键字。 堆分为大顶堆和小顶堆，满足Key[i]>=Key[2i+1]&&key>=key[2i+2]称为大顶堆，满足 Key[i]<=key[2i+1]&&Key[i]<=key[2i+2]称为小顶堆。由上述性质可知大顶堆的堆顶的关键字肯定是所有关键字中最大的，小顶堆的堆顶的关键字是所有关键字中最小的。

2.堆排序的思想

利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性，使得每次从无序中选择最大记录(最小记录)变得简单。 其基本思想为(大顶堆)： 1)将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆，此堆为初始的无序区； 2)将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n]; 3)由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。 操作过程如下： 1)初始化堆：将R[1..n]构造为堆； 2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换，然后将新的无序区调整为新的堆。 因此对于堆排序，最重要的两个操作就是构造初始堆和调整堆，其实构造初始堆事实上也是调整堆的过程，只不过构造初始堆是对所有的非叶节点都进行调整。

3.一个图示实例

给定一个整形数组a[]={16,7,3,20,17,8}，对其进行堆排序。 首先根据该数组元素构建一个完全二叉树，得到 

20和16交换后导致16不满足堆的性质，因此需重新调整

这样就得到了初始堆。

先进行一次调整时其成为大顶堆，

即每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换(交换之后可能造成被交换的孩子节点不满足堆的性质，因此每次交换之后要重新对被交换的孩子节点进行调整)。有了初始堆之后就可以进行排序了。

此时3位于堆顶不满堆的性质，则需调整继续调整  

 这样整个区间便已经有序了。从上述过程可知，堆排序其实也是一种选择排序，是一种树形选择排序。只不过直接选择排序中，为了从R[1...n]中选择最大记录，需比较n-1次，然后从R[1...n-2]中选择最大记录需比较n-2次。事实上这n-2次比较中有很多已经在前面的n-1次比较中已经做过，而树形选择排序恰好利用树形的特点保存了部分前面的比较结果，因此可以减少比较次数。对于n个关键字序列，最坏情况下每个节点需比较log2(n)次，因此其最坏情况下时间复杂度为nlogn。堆排序为不稳定排序，不适合记录较少的排序。 上面描述了这么多，简而言之,堆排序的基本做法是:首先，用原始数据构建成一个大(小)堆作为原始无序区，然后，每次取出堆顶元素，放入有序区。由于堆顶元素被取出来了，我们用堆中最后一个元素放入堆顶，如此，堆的性质就被破坏了。我们需要重新对堆进行调整，如此继续N次，那么无序区的N个元素都被放入有序区了，也就完成了排序过程。

4.堆排序算法伪代码(来自算法导论）

1.下标计算[为与程序对应，下标从0开始]
Parent(i)://为了伪代码描述方便
    returni/2
Left(i):
    return2*i+1
Right(i):
    return2*i+2
2.使下标i元素为根的的子树成为最大堆
MAX_HEAPIFY(A,i):
l<——Left(i)
r<——Right(i)
ifl<length(A)andA[l]>A[i]
    thenlargest<——l
    elselargest<——i
ifr<length(A)andA[r]>A[largest]
    thenlargest<——r
iflargest!=i
    thenexchangeA[i]<——>A[largest]//到这里完成了一层下降
    MAX_HEAPIFY(A,largest)//这里是递归的让当前元素下降到最低位置
3.最大堆的建立,将数组A编译成一个最大堆
BUILD_MAX_HEAP(A):
    heapsize[A]<——length[A]
fori<——length[A]/2+1  to0
    MAX_HEAPIFY(A,i)//堆排序的开始首先要构造大顶堆，这里就是对内层节点进行逐级下沉（小元素）
4.堆排序
HEAP_SORT(A):
    BUILD_MAX_HEAP(A)
    fori<——length[A]-1to1//这里能够保证堆大小和数组大小的关系，堆在每一次置换后都减一
        doexchangeA[1]<——>  A[i]
        length[A]<——length[A]-1
        MAX_HEAPIFY(A,0)//对交换后的元素下沉

5.堆排序代码实现

#include <stdio.h>
#include <stdio.h>
#include <stdlib.h>
#define PARENT(i) (i)/2
#define LEFT(i) 2*(i)+1
#define RIGHT(i) 2*(i+1)
 
voidswap(int*a,int*b)
{
    *a=*a^*b;  
    *b=*a^*b;  
    *a=*a^*b;  
}
voidmax_heapify(int*arr,intindex,intlen)
{
    intl=LEFT(index);
    intr=RIGHT(index);
    intlargest;
    if(l<len&&arr[l]>arr[index])
        largest=l;
    else
        largest=index;
    if(r<len&&arr[r]>arr[largest])
        largest=r;
    if(largest!=index){//将最大元素提升，并递归
        swap(&arr[largest],&arr[index]);
        max_heapify(arr,largest,len);
    }
}
 
voidbuild_maxheap(int*arr,intlen)
{
    inti;
    if(arr==NULL||len<=1)
        return;
    for(i=len/2+1;i>=0;--i)
        max_heapify(arr,i,len);
}
voidheap_sort(int*arr,intlen)
{
    inti;
    if(arr==NULL||len<=1)
        return;
    build_maxheap(arr,len);
 
    for(i=len-1;i>=1;--i){
        swap(&arr[0],&arr[i]);
        max_heapify(arr,0,--len);
    }
}
 
intmain()
{
    intarr[10]={1,4,6,2,5,8,7,6,9,12};
    inti;
    heap_sort(arr,10);
    for(i=0;i<10;++i)
        printf("%d ",arr[i]);
    system("pause");
}

 6.堆排序算法复杂度

重新调整堆的时间复杂度为O(logN)，共N – 1次重新恢复堆操作，再加上前面建立堆时N / 2次向下调整，每次调整时间复杂度也为O(logN)，二者相加还是O(N * logN)。故堆排序的时间复杂度为O(N * logN)。