SOURCE：NOIP2016-RZZ-1 T3

题目描述

有一个 2×N 的矩阵，矩阵的每个位置上都是一个英文小写字符。

现在需要从某一个位置开始，每次可以移动到一个没有到过的相邻位置，即从 (i,j) 可以移动到 (i-1,j)(i+1,j)(i,j-1)(i,j+1) （要求该位置在矩阵上且之前没有到过）。

从选取的起点开始，经过 2N-1 次移动后，将会走过矩阵的每一个位置，将移动经过的格子依次取出来就得到了一个长度为 2N 的串。

可以任意选择起点和终点，任意选择移动方案，求能得到多少种不同的串。

输入格式

输入第一行，一个正整数 N 。
接下来两行，每行一个由英文小写字符组成的字符串，描述这个矩阵。

输出格式

输出一行一个整数，表示能得到的串的总数。

样例数据 1

输入

1
a
a

输出

1

样例数据 2

输入

3
dab
abd

输出

8

样例数据 3

输入

5
ababa
babab

输出

2

备注

【样例2说明】

技术分享

能得到的字符串有：abdbad, adabdb, badabd, bdbada, dababd, dabdba, dbabad, dbadab。

【数据规模与约定】

对于 20% 的数据，N≤5。
对于 60% 的数据，N≤50。
对于 100% 的数据，N≤600。

【题目分析】

没怎么做过字符串哈希的题目，这次就当是预习了。

因为题目中要求不能走已经走过的地方，并且要将整个矩阵走完，那么整个问题就有套路了。

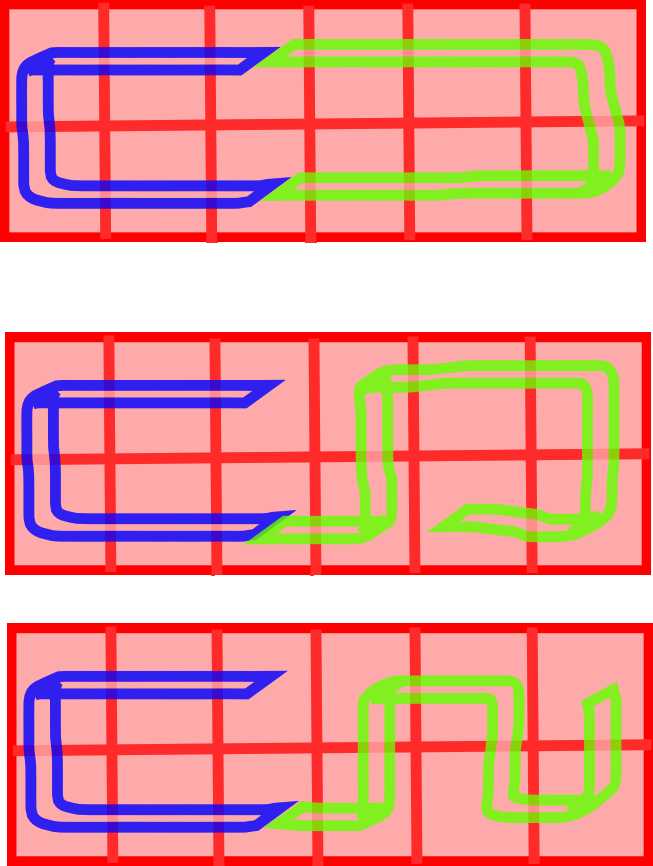
走法都是固定的：

从某一点出发，向左或向右走到头，再拐回到同一列，然后从下一列开始可以选择走若干个蛇形（可以是$0$），然后迂回。

如下图所示：

技术分享

$........$

当然方向不止这几种，哈希时进行$4$次反转即可。

下面来看看哈希：

整个图形可以看成三部分：左边迂回的部分，中间蛇形的部分，右边迂回的部分。

我们可以将左边迂回部分的哈希值预处理出来，然后枚举右边迂回的部分，每次拼接一个蛇形，再拼接上左边的部分。

注意在将右边和蛇形与左边拼接时，因为已经预处理出了左边，所以只需将右边加蛇形的哈希值乘上$Powh[2 * (j - 1)]$再加上左边的哈希值（j的含义看代码，具体为什么乘以可以试着写写没有预处理时的计算式子）。

【CODE】

　　下面是单哈希的代码。

#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<cstdlib>
#include<algorithm>
#include<vector>
using namespace std;

const int h = 2333, H = 2333333;
int n;
char s[5][2000];
unsigned long long num[6000600];
unsigned long long l[5][2000];
unsigned long long Powh[2000];
unsigned long long now;
int fst[2400000], nxt[6000600], tot;

inline void insert(unsigned long long x){
    int i, y = x % H;
    for(i = fst[y]; i; i = nxt[i])
        if(num[i] == x) return;
    num[++tot] = x;
    nxt[tot] = fst[y];
    fst[y] = tot;
}

int main(){
    int i, j; 
    for(Powh[0] = i = 1; i <= 1300; i++)
        Powh[i] = Powh[i - 1] * h;
    scanf("%d", &n);
    scanf("%s", s[1] + 1);
    scanf("%s", s[2] + 1);
    tot = 0;
    for(int T = 1; T <= 4; T++){
        for(i = 1; i <= n; i++){
            l[1][i] = l[2][i] = 0;
            for(j = i; j >= 1; j--) l[1][i] = l[1][i] * h + s[1][j];
            for(j = 1; j <= i; j++) l[1][i] = l[1][i] * h + s[2][j]; 
            for(j = i; j >= 1; j--) l[2][i] = l[2][i] * h + s[2][j];
            for(j = 1; j <= i; j++) l[2][i] = l[2][i] * h + s[1][j];
        }
        int k;
        for(i = 1; i <= n; i++){
            now = 0;
            for(j = i; j <= n; j++) now = now * h + s[1][j];
            for(j = n; j >= i; j--) now = now * h + s[2][j];
            k = 2;
            for(j = i; j >= 1; j--){
                insert(l[k][j - 1] + now * Powh[2 * (j - 1)]);
                now = now * h + s[k][j - 1];
                k = 3 - k;
                now = now * h + s[k][j - 1];
            }
        }
        
        for(i = 1; i <= n; i++) swap(s[1][i], s[2][i]);
        if(T == 2){
            for(i = 1; i <= n / 2; i++){
                swap(s[1][n - i + 1] , s[1][i]);
                swap(s[2][n - i + 1] , s[2][i]);
            }
        }
    }
    cout<<tot<<endl;
    return 0;
}

View Code

【NOIP模拟】Grid（字符串哈希）

题目背景