我们探讨的情况下，我们使用一个参数θ1和绘制其成本函数来实现梯度下降。我们对一个参数的公式是
重复直至收敛：
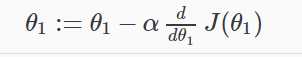
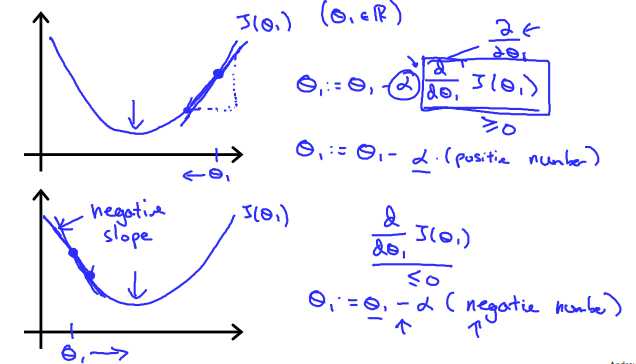
不管斜坡的标志
是什么，θ1最终收敛到最小值。下面的图表显示，当斜率为负，价值θ1增加当它是正的，对θ1值减
另一方面，我们应该调整参数α，以确保梯度下降算法在合理的时间内收敛。未能收敛或太多的时间来获得最小值意味着我们的步长是错误的.
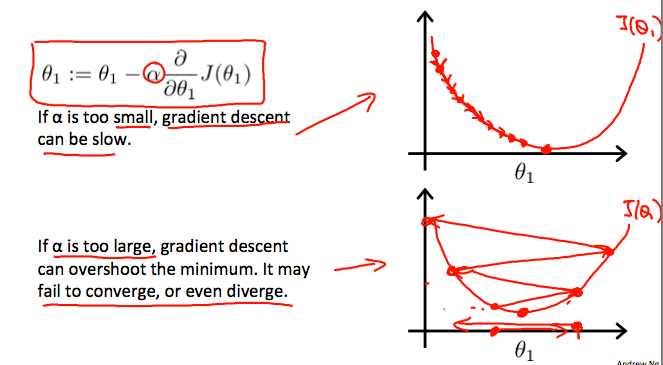
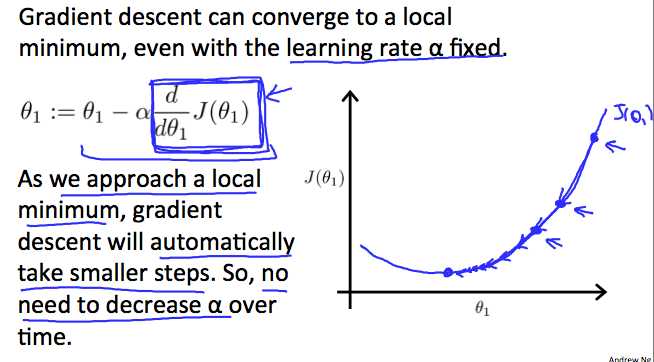
梯度下降是如何与固定步长α收敛的。
在收敛的直觉是
接近0我们的凸函数的底。至少，导数总是0，这样我们就可以得到：
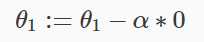
原文：http://www.cnblogs.com/zhengzhe/p/7223688.html