loj.ac上有 题目传送门
不过我还是把题目搬过来吧
整数(integer)
【题目背景】
在人类智慧的山巅,有着一台字长为 1048576 位的超级计算机,著名理论计算机科 学家 P 博士正用它进行各种研究。不幸的是,这天台风切断了电力系统,超级计算机 无法工作,而 P 博士明天就要交实验结果了,只好求助于学过 OI 的你......
【题目描述】 P 博士将他的计算任务抽象为对一个整数的操作。
具体来说,有一个整数 x ,一开始为 0。 接下来有 n 个操作,每个操作都是以下两种类型中的一种:
? 1 a b :将 x 加上整数 a·2b,其中 a 为一个整数,b 为一个非负整数
? 2 k :询问 x 在用二进制表示时,位权为 2k 的位的值(即这一位上的 1 代表 2k )
保证在任何时候,x≥0。
【输入格式】 从标准输入读入数据。
输入的第一行包含四个正整数 n,t1,t2,t3,n 的含义见题目描述,t1,t2,t3 的具体含义 见子任务。
接下来 n 行,每行给出一个操作,具体格式和含义见题目描述。
同一行输入的相邻两个元素之间,用恰好一个空格隔开。
【输出格式】
输出到标准输出。
对于每个询问操作,输出一行,表示该询问的答案(000 或 111)。 对于加法操作,没有任何输出
10 3 1 2
1 100 0
1 2333 0
1 -233 0
2 5
2 7
2 15
1 5 15
2 15
1 -1 12
2 15
【样例 1 输出】
0
1
0
1
0

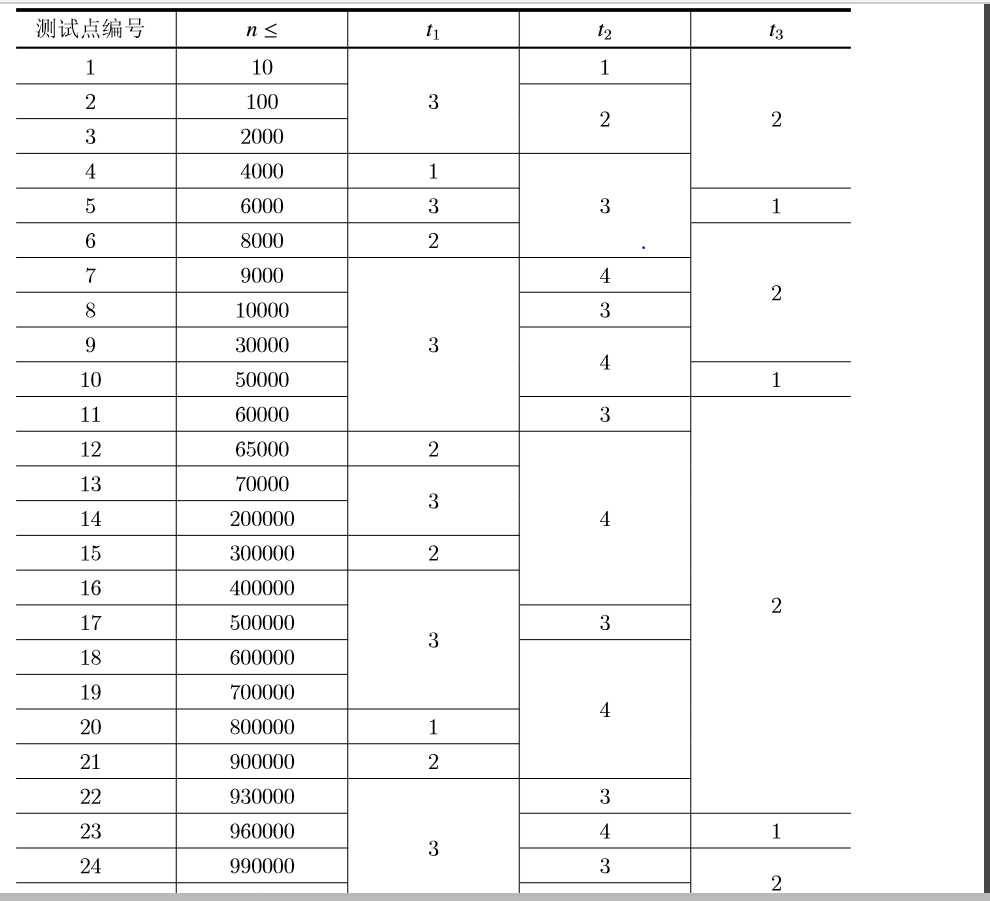
【子任务】 在所有测试点中,
1 ≤ t1 ≤ 3,1 ≤ t2 ≤ 4,1 ≤ t3 ≤ 2。
不同的 t1,t2,t3 对应的特殊限制 如下:
? 对于 t1 = 1 的测试点,满足 a = 1
?对于 t1 = 2 的测试点,满足 |a|= 1
? 对于 t1 = 3 的测试点,满足 |a|≤109 ? 对于 t2 = 1 的测试点,满足 0≤b,k≤30
? 对于 t2 = 2 的测试点,满足 0≤b,k≤100
? 对于 t2 = 3 的测试点,满足 0≤b,k≤n
? 对于 t2 = 4 的测试点,满足 0≤b,k≤30n
? 对于 t3 = 1 的测试点,保证所有询问操作都在所有修改操作之后
? 对于 t3 = 2 的测试点,不保证询问操作和修改操作的先后顺序
这道题首先 a*2^b 这个东西呢按我的想法是把 a 拆成2的x次幂的和 然后+b
如果只有加法当然很好写 但是这道题 a 可能是负的
所以我开了两个数组 s1 s2 来存 s1 存的是正的 s2 存的是负的
注意存的时候进位 均摊复杂度只有o(1) 所以暴力进位就好了
然后问题就转换成了已知两个高精度数,问他们的差的某一位是什么
然后分类可得
我们记一个数为 1(0)x
1 (0) 表示询问的这一位的值(因为是二进制,所以不是1就是0)
x就是询问位后面那一串东西(一坨1 0 混合体)
考虑减法是否退位的时候呢
1. x>=y:
1x-1y=0(x-y)
1x-0y=1(x-y)
0x-1y=1(x-y)
0x-0y=0(x-y)
2. x<y:
1x-1y=1(x-y+2^k)
1x-0y=0(x-y+2^k)
0x-1y=0(x-y+2^k)
0x-0y=1(x-y+2^k)
举个例子吧
10-10=00
10-00=10
01-10=11
01-01=00
10-11=11
10-01=01
00-11=01
00-01=11
注 题目保证x始终大于等于0 所以s1总和也一定大于s2
这样分析之后呢 问题就转换成了从1-x(即询问位)-1这个区间里s1 s2 的大小关系
如果 s1>=s2
那么答案就是 s1^s2(^念做异或)
如果 s2<=s2
那么答案就是 s1==s2 (==念做同或)
那么 x 和 y 的比较 其实就是比较字典序 找到第一个不一样的地方 哪个是1 哪个就大 (这么很好证明我就不详细讲了) 注意这里讲的都是二进制
算了举个例子吧 如果x是1000 y是0111 那么x是不是一定大于y
所以我们可以采用线段树维护区间内s1 s2 的大小
当然我这里采用的是zkw线段树 (自带底层优化自然会比较快 而且修改也很好写)
毕竟三千万(3e7)个叶子结点 同时线段树中下标也就是二进制中 2的次数
操作自然就是 区间内单点修改,前缀查询
那么我们每次操作1拆完a加上b以及进位之后
我们要记录一波 修改到的最左位置到最右位置 进位自然也算修改
然后就在线段树上暴力修改顺便上传信息 复杂度是 o( r-l + log(n))
操作2 询问的时候我们就找到区间中靠右(也就是比较大的位置)的第一个不一样的地方然后判断一波就好了
到这里题目就完美解决了 修改(modify)以及 查找(find) 就看代码吧
注: find我的写法呢 是向上走时,如果x是右孩子且x的兄弟为1才向下走
实测跑得也蛮快的 23333


#include<cstdio> #include<cstring> #include<algorithm> #include<cmath> #define LL long long using namespace std; const int M=3e7+31,N=1<<25; int read(){ int ans=0,f=1,c=getchar(); while(c<‘0‘||c>‘9‘){if(c==‘-‘) f=-1; c=getchar();} while(c>=‘0‘&&c<=‘9‘){ans=ans*10+(c-‘0‘); c=getchar();} return ans*f; } int s1[M],s2[M],cnt; int l,r,a,b,n,k; void prepare(int x){ if(!x) return ; int v=x>0?x:-x,w[31]; cnt=0; for(int i=30;i>=0;i--){ int now=1<<i; if(now&v) v-=now,w[++cnt]=i; if(!v) break; } l=w[cnt]+b; r=w[1]+b; if(x>0) for(int i=1;i<=cnt;i++){ int now=w[i]+b; while(s1[now]) s1[now++]=0,r=max(r,now); s1[now]=1; } else for(int i=1;i<=cnt;i++){ int now=w[i]+b; while(s2[now]) s2[now++]=0,r=max(r,now); s2[now]=1; } } int tr[2*N],T,now; void modify(){ for(int i=l;i<=r;i++) tr[i+N]=s1[i]^s2[i]; for(l=(l+N)>>1,r=(r+N)>>1;l;l>>=1,r>>=1) for(int i=l;i<=r;i++) tr[i]=tr[i<<1]|tr[i<<1^1]; } int find(int k){ for(k+=N;k;k>>=1) if(k&1&tr[k^1]){ for(k^=1;k<N;k=k<<1^tr[k<<1^1]); return k-N; } return -1; } int main() { n=read(); T=read(); T=read(); T=read(); for(int i=1;i<=n;i++){ k=read(); if(k==1){ a=read(); b=read(); prepare(a); modify(); } else{ a=read(); now=find(a); if(s1[now]>s2[now]||now==-1) printf("%d\n",s1[a]^s2[a]); else printf("%d\n",s1[a]==s2[a]); } } return 0; }
原文:http://www.cnblogs.com/lyzuikeai/p/7224090.html