梯度下降提供了一种最小化J的方法。让我们讨论第二种方法,这一次显式地执行最小化,而不用迭代算法。在“方程”的方法,我们将最大限度地减少J通过明确其衍生物相对于θJ的,并使其为零。这使我们能够在没有迭代的情况下找到最佳θ。下面给出正规方程公式。
![]()
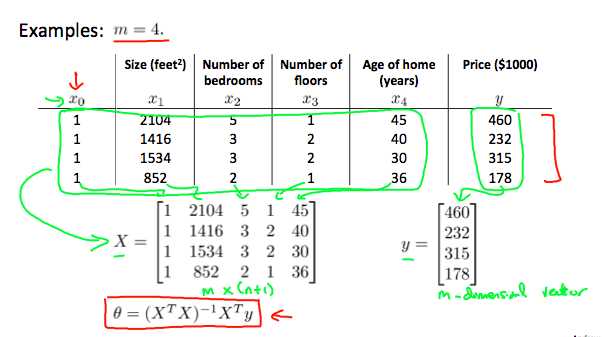
正规方程不需要进行特征缩放。
下面是梯度下降和正规方程的比较:

用正规方程计算,时间复杂度为O(n^3)。因此,如果我们有大量的特征,正常的方程将是缓慢的。实际上,当n超过10000时,可能是从正常解决方案到迭代过程的好时机。
原文:http://www.cnblogs.com/zhengzhe/p/7224635.html