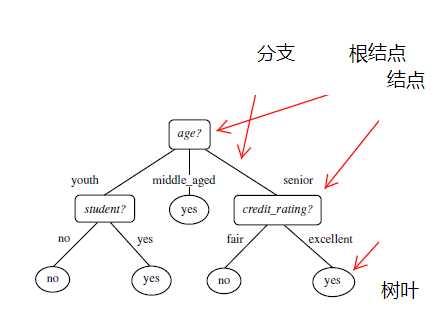
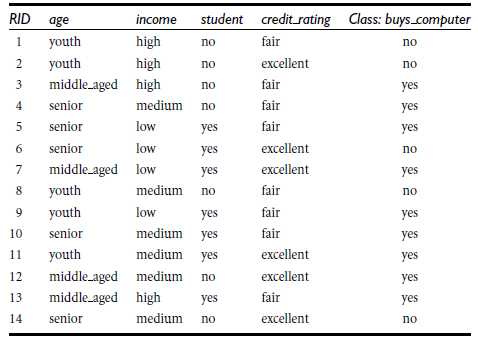
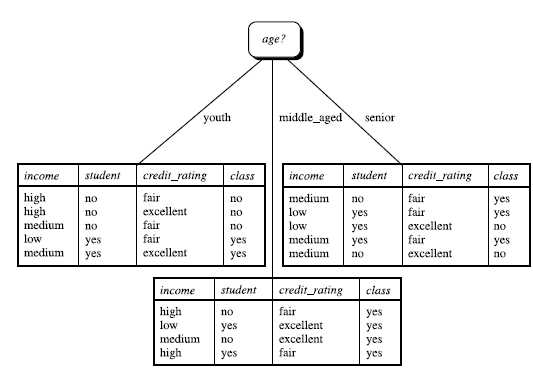
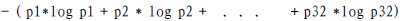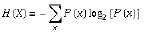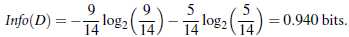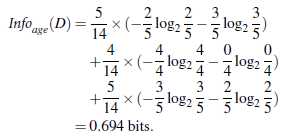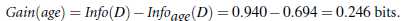1. 什么是决策树/判定树(decision tree)?
判定树是一个类似于流程图的树结构:其中,每个内部结点表示在一个属性上的测试,每个分支代表一个属性输出,而每个树叶结点代表类或类分布。树的最顶层是根结点。
2. 机器学习中分类方法中的一个重要算法
3. 构造决策树的基本算法
3.1 熵(entropy)概念:
信息和抽象,如何度量?
1948年,香农提出了 ”信息熵(entropy)“的概念
一条信息的信息量大小和它的不确定性有直接的关系,要搞清楚一件非常非常不确定的事情,或者
是我们一无所知的事情,需要了解大量信息==>信息量的度量就等于不确定性的多少
例子:猜世界杯冠军,假如一无所知,猜多少次?
每个队夺冠的几率不是相等的
比特(bit)来衡量信息的多少
变量的不确定性越大,熵也就越大
3.1 决策树归纳算法 (ID3)
1970-1980, J.Ross. Quinlan, ID3算法
选择属性判断结点
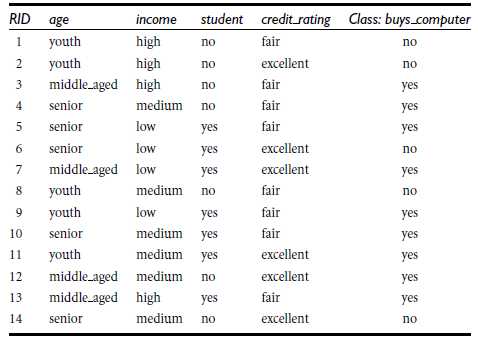
信息获取量(Information Gain):Gain(A) = Info(D) - Infor_A(D)
通过A来作为节点分类获取了多少信息
类似,Gain(income) = 0.029, Gain(student) = 0.151, Gain(credit_rating)=0.048
所以,选择age作为第一个根节点
重复。。。
算法:
- 树以代表训练样本的单个结点开始(步骤1)。
- 如果样本都在同一个类,则该结点成为树叶,并用该类标号(步骤2 和3)。
- 否则,算法使用称为信息增益的基于熵的度量作为启发信息,选择能够最好地将样本分类的属性(步骤6)。该属性成为该结点的“测试”或“判定”属性(步骤7)。在算法的该版本中,
- 所有的属性都是分类的,即离散值。连续属性必须离散化。
- 对测试属性的每个已知的值,创建一个分枝,并据此划分样本(步骤8-10)。
- 算法使用同样的过程,递归地形成每个划分上的样本判定树。一旦一个属性出现在一个结点上,就不必该结点的任何后代上考虑它(步骤13)。
- 递归划分步骤仅当下列条件之一成立停止:
- (a) 给定结点的所有样本属于同一类(步骤2 和3)。
- (b) 没有剩余属性可以用来进一步划分样本(步骤4)。在此情况下,使用多数表决(步骤5)。
- 这涉及将给定的结点转换成树叶,并用样本中的多数所在的类标记它。替换地,可以存放结
- 点样本的类分布。
- (c) 分枝
- test_attribute = a i 没有样本(步骤11)。在这种情况下,以 samples 中的多数类
- 创建一个树叶(步骤12)
3.1 其他算法:
C4.5: Quinlan
Classification and Regression Trees (CART): (L. Breiman, J. Friedman, R. Olshen, C. Stone)
共同点:都是贪心算法,自上而下(Top-down approach)
区别:属性选择度量方法不同: C4.5 (gain ratio), CART(gini index), ID3 (Information Gain)
3.2 如何处理连续性变量的属性?
4. 树剪枝叶 (避免overfitting)
4.1 先剪枝
4.2 后剪枝
5. 决策树的优点:
直观,便于理解,小规模数据集有效
6. 决策树的缺点:
处理连续变量不好
类别较多时,错误增加的比较快
可规模性一般
代码部分:
1、运行环境
#!/usr/bin/python
# encoding: utf-8
"""
@author : 杜函敏
@File : AllElectronics.py
@time : 2017/7/23 16:45
"""
from sklearn.feature_extraction import DictVectorizer
import csv
from sklearn import tree
from sklearn import preprocessing
from sklearn.externals.six import StringIO
import pydotplus
2、载入文件
allElectronicsData = open(‘C:/Users/007/Desktop/01DTree/AllElectronics.csv‘)
reader = csv.reader(allElectronicsData)
headers = next(reader) #取出标题
3、提取数据
featureList = []
labelList = []
for row in reader:
labelList.append(row[len(row)-1]) #取最后一列
rowDict = {}
for i in range(1, len(row)-1):
rowDict[headers[i]] = row[i] #将数据保存为字典,不含最后一列
featureList.append(rowDict)
4、数据处理为方便运算的形式
# 非数值类型变为数值矩阵
vec = DictVectorizer()
dummyX = vec.fit_transform(featureList) .toarray()
print("dummyX: " + str(dummyX))
print(vec.get_feature_names())
print("labelList: " + str(labelList))
# yes和no转化为0和1
lb = preprocessing.LabelBinarizer()
dummyY = lb.fit_transform(labelList)
print("dummyY: " + str(dummyY))
5、模型生成与画图
# 使用决策树进行分类clf = tree.DecisionTreeClassifier()
clf = tree.DecisionTreeClassifier(criterion=‘entropy‘)
clf = clf.fit(dummyX, dummyY)
print("clf: " + str(clf))
# 生成决策树pdf图
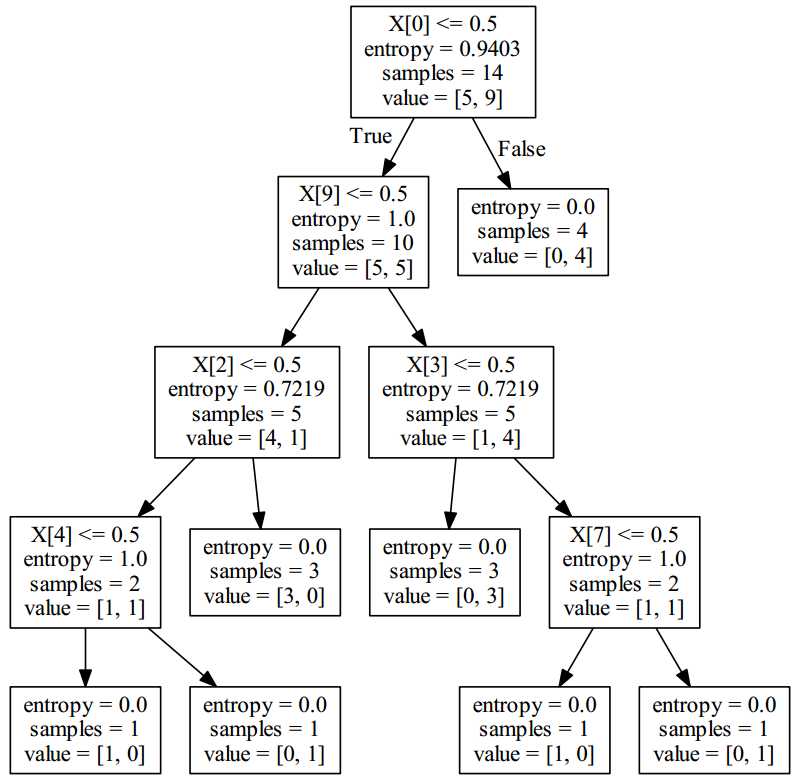
dot_data = tree.export_graphviz(clf, out_file=None)
graph = pydotplus.graph_from_dot_data(dot_data)
graph.write_pdf("iris.pdf")
6、验证模型
#拿第一行数据进行修改,测试模型结果
oneRowX = dummyX[0, :]
print("oneRowX: " + str(oneRowX))
newRowX = oneRowX
newRowX[0] = 1
newRowX[2] = 0
print("newRowX: " + str(newRowX))
predictedY = clf.predict(newRowX.reshape(1, -1)) #需要将数据reshape(1, -1)处理
print("predictedY: " + str(predictedY))
结果图:
决策树分类算法(ID3)
原文:http://www.cnblogs.com/duhanmin/p/7225255.html