我们可以讨论分类问题,忽略y是离散值这一事实,并使用我们的旧线性回归算法来预测y给定x。然而,很容易构造例子,这种方法表现很差。直观地说,也没有道理当h(θ)(x)取值大于1或小于0时,我们知道,Y∈{ 0, 1 }。为了解决这个问题,让我们改变我们的假设H(θ)(x)满足0≤h(θ)(x)≤1。这是通过将θTx插入到逻辑函数中来实现的。
我们的新形式使用了“S函数”,也称为“逻辑函数”:
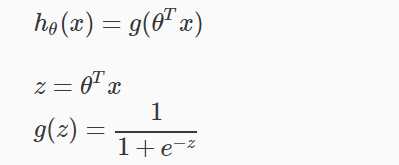
下图显示了S形函数是什么样子的:

这里所示的函数g(z)将任意实数映射到(0, 1)区间,使得它可以用于将任意值函数转换为更适合于分类的函数。
Hθ(x)会给我们输出的概率是1。例如,Hθ(x)= 0.7给了我们一个70%的概率,我们的产量是1。我们的预测是0的概率正好是我们的概率为1的补充(例如,如果概率是1是70%,那么它是0的概率是30%)
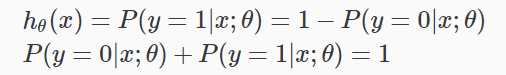
原文:http://www.cnblogs.com/zhengzhe/p/7225204.html