
【题目描述】 新牛到部队,CG 要求它们每天早上搞晨跑,从 A 农场跑到 B 农场。从 A 农场到 B 农场中有 n-2 个路口,分别标上号,A 农场为 1 号,B 农场为 n 号,路口分别为 2...n-1 号,从 A 农场到 B 农场有很多条路径可以到达,而 CG 发现有的路口是必须经过的,即每条路径都经过的路口,CG 要把它们记录下来,这样 CG 就可以先到那个路口,观察新牛们有没有偷懒,而你的任务就是找出所有必经路口。 【输入格式】 第一行两个用空格隔开的整数 n(3≤n≤2000)和 e(1≤e≤8000)。 接下来从第 2 到第 e+1 行,每行两个用空格隔开的整数 p 和 q,表示路口 p 和 q 之间有路径直达。 输入数据保证必经路口一定存在,并且每个路口都和 A 农场、B 农场相连通。 【输出格式】 第一行一个整数 m,表示必经路口的数目。 第二行按从小到大的顺序依次输出每个必经路口的编号,每两个数之间用一个空格隔 开。 注意:不包括起点和终点。 【输入样例】 6 6 1 2 2 4 2 3 3 5 4 5 5 6 【输出样例】 2 2 5
tag:dfs
思路:如果一个点是必须经过的,那么如果没有它,点1和点n将不会连通。可以用floyd,但时间不能保证,所以选择dfs。这里要注意,做这道题不能用以往的dfs套路,也就是说不能回溯。
1 #include<cstdio> 2 #include<algorithm> 3 #include<iostream> 4 #include<cmath> 5 #define maxn 2010 6 using namespace std; 7 int n,m,vis[maxn],cnt,ans[maxn],Ans,hl[maxn],f; 8 struct X{ 9 int u,v,ne; 10 }e[maxn<<4]; 11 int read() 12 { 13 int x=0,flag=1; 14 char ch=getchar(); 15 while(ch<‘0‘||ch>‘9‘){ 16 if(ch==‘-‘) flag=-1; 17 ch=getchar(); 18 } 19 while(ch>=‘0‘&&ch<=‘9‘){ 20 x=x*10+ch-‘0‘; 21 ch=getchar(); 22 } 23 return x*flag; 24 } 25 void add(int x,int y) 26 { 27 e[++cnt].u=x; 28 e[cnt].v=y; 29 e[cnt].ne=hl[x]; 30 hl[x]=cnt; 31 } 32 void dfs(int x) 33 { 34 if(vis[n]) return; 35 vis[x]=1; 36 if(x==n) return; 37 for(int j=hl[x];j;j=e[j].ne){ 38 int v=e[j].v; 39 if(!vis[v]) dfs(v); 40 } 41 } 42 int main() 43 { 44 //freopen("running.in","r",stdin); 45 //freopen("running.out","w",stdout); 46 int x,y; 47 scanf("%d%d",&n,&m); 48 for(int i=1;i<=m;++i){ 49 x=read();y=read(); 50 add(x,y); 51 add(y,x); 52 } 53 for(int i=2;i<n;++i){ 54 memset(vis,0,sizeof(vis)); 55 vis[i]=1; 56 f=0; 57 dfs(1); 58 if(!vis[n]){ 59 ans[i]=1; 60 Ans++; 61 } 62 vis[i]=0; 63 } 64 printf("%d\n",Ans); 65 for(int i=1;i<=n;++i) if(ans[i]) printf("%d ",i); 66 return 0; 67 }

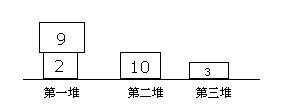
【问题描述】 陈老师喜欢网购书籍,经常一次购它个百八十本,然后拿来倒卖,牟取暴利。前些天,高一的新同学来了,他便像往常一样,兜售他的书,经过一番口舌,同学们决定买他的书,但是 CS 桌上的书有三堆,每一堆都有厚厚的一叠,他要想个办法用最轻松的方式把书拿下来给同学们.但是你想逗一下 CS,于是,请你设计一个最累的方式给他. 若告诉你这三堆分别有 i,j,k 本书,以及每堆从下到上书的重量.每次取书只能从任意一堆的最上面取,那么请你帮助他设计一个方案,让他花最大的力气取下所有书(CS 别打我). 显然,每次取书,陈老师的体力消耗都会加大,这里用体力系数代表,取下第一本书时,体力系数为 1,第二本时为 2,依次类推,而每次体力消耗值则为体力系数和书的重量之积。 举个例子: 三堆书及重量如下 (配图在外) 不用证明,最累的取书方式为: 右左左中, 即: 3*1+9*2+2*3+10*4=3+18+6+40=67 【输入文件】(book.in) 输入文件的第一行为 3 个数,分别为三堆数量 I,j,k 第二行至第四行分别为每堆由下至上的书本重量 【输出文件】(book.out) 输出最累方式的体力消耗总值即可 【输入样例】 3 2 4 2 3 2 1 5 9 8 7 4 【输出样例】 257 【注释】: 输入数据为每堆由下至上的书本重量! 【数据规模】 对于 40%的数据有:0<=i<10 0<=j<10 0<=k<10 对于 100%的数据有:0<=i<100 0<=j<100 0<=k<100 最后输出的体力消耗总值在 longint 范围内
tag:背包DP
思路:一道比较基础的DP,需要准确找到继承关系。我们用f[i][j][k]表示选择i本第一堆的书+j本+k本的最优解,可得dp方程f[i][j][k]=max(f[i][j][k],f[i-1][j][k]+a1[i]*(i+j+k),f[i][j-1][k]+a2[j]*(i+j+k),f[i][j][k-1]+a3[k]*(i+j+k));
1 #include<cstdio> 2 #include<algorithm> 3 #include<iostream> 4 #include<cmath> 5 #include<stack> 6 using namespace std; 7 long f[110][110][110]; 8 int a1[110],a2[110],a3[110],k1,k2,k3,i,j,k; 9 int main() 10 { 11 //freopen("book.in","r",stdin); 12 //freopen("book.out","w",stdout); 13 scanf("%d%d%d",&k1,&k2,&k3); 14 for(i=k1;i>0;--i) scanf("%d",&a1[i]); 15 for(i=k2;i>0;--i) scanf("%d",&a2[i]); 16 for(i=k3;i>0;--i) scanf("%d",&a3[i]); 17 for(i=0;i<=k1;++i) 18 for(j=0;j<=k2;++j) 19 for(k=0;k<=k3;++k){ 20 if(i>=1) f[i][j][k]=max(f[i][j][k],f[i-1][j][k]+a1[i]*(i+j+k)); 21 if(j>=1) f[i][j][k]=max(f[i][j][k],f[i][j-1][k]+a2[j]*(i+j+k)); 22 if(k>=1) f[i][j][k]=max(f[i][j][k],f[i][j][k-1]+a3[k]*(i+j+k)); 23 } 24 printf("%ld\n",f[k1][k2][k3]); 25 return 0; 26 }

【问题描述】 英语四级考试临近了,小 Y 却发现他已经把以前学的单词几乎忘光了。好在现在离考试还有一段时间,小 Y 决定从现在开始夜以继日地背单词。也就是说小 Y 废寝忘食,一天二十四小时地背单词。 今天的日期(时间)是 YYYY 年 mm 月 dd 日 hh 时 min 分,考试的时间是 YYYY’年 mm’月dd’日 hh’时 min’分。这之间的所有时间小 Y 都用来背单词了,那么考试之前他最多能背多少个单词呢? 时间紧张,小 Y 只管数量不管质量。当然有的单词长一些,有的单词短一些。长的单词难背一些,短的单词好背一些。根据小 Y 的经验,他能一眼看出背某一个单词需要的时间,以分钟记。 现在给你一个字典,请你挑出最多的单词使小 Y 能在考试前背出来。【输入格式】 第一行一个整数 N,表示字典中的单词数,N<=5000。 接下来 N 行,每行一个整数表示背这个单词需要用的时间,以分钟记,小于等于 10000。(这个单词本身是什么并不重要,不是吗?当前小 Y 已经认识的单词数为 0 个)。 接下来两行依次是当前时问和考试时间。时间给出的格式是:yyyy-mm-dd-hh:min.例 如:2007-06-23-02:00,采用 24 小时制,每天从 00:00-23:59,年份从 0000 到 9999。 【输出格式】 一行一个数,表示考试前小 Y 最多能背出的单词数:【输入样例】 2 1 1 2007-06-23-11:59 2007-06-23-12:00 【样例输出】 1
tag:模拟 贪心
思路:直接算两个点的时间差需要无数个特判,难度太大,应转为从0000年的起始时间点开始计算,取整年整月比较好算。注意闰年。
1 #include<cstdio> 2 #include<algorithm> 3 #include<iostream> 4 #include<cmath> 5 #include<queue> 6 using namespace std; 7 priority_queue<int>Q; 8 int cnt,n,x,ans,yue[15]={0,31,28,31,30,31,30,31,31,30,31,30,31},run[10010],c[10010]; 9 long long t,t1,t2; 10 struct X 11 { 12 int year,month,day,hour,min; 13 }a,b; 14 int read() 15 { 16 int x=0,flag=1; 17 char ch=getchar(); 18 while(ch<‘0‘||ch>‘9‘){ 19 if(ch==‘-‘) flag=-1; 20 ch=getchar(); 21 } 22 while(ch>=‘0‘&&ch<=‘9‘){ 23 x=x*10+ch-‘0‘; 24 ch=getchar(); 25 } 26 return x*flag; 27 } 28 void dabiao() 29 { 30 for(int i=0;i<=9999;++i) 31 if(i%4==0){ 32 run[i]=1; 33 if((i%100==0)&&(i%400!=0)) run[i]=0; 34 } 35 } 36 void work() 37 { 38 t1=t2=0; 39 for(int i=0;i<a.year;++i) t1+=(365+run[i])*1440; 40 for(int i=1;i<a.month;++i) t1+=yue[i]*1440; 41 t1+=(a.day-1)*1440; 42 t1+=a.hour*60; 43 t1+=a.min; 44 for(int i=0;i<b.year;++i) t2+=(365+run[i])*1440; 45 for(int i=1;i<b.month;++i) t2+=yue[i]*1440; 46 t2+=(b.day-1)*1440; 47 t2+=b.hour*60; 48 t2+=b.min; 49 t=t2-t1; 50 } 51 int main() 52 { 53 //freopen("words.in","r",stdin); 54 //freopen("words.out","w",stdout); 55 dabiao(); 56 scanf("%d",&n); 57 for(int i=1;i<=n;++i) scanf("%d",&c[i]); 58 sort(c+1,c+n+1); 59 a.year=read();a.month=read();a.day=read();a.hour=read();a.min=read(); 60 b.year=read();b.month=read();b.day=read();b.hour=read();b.min=read(); 61 work(); 62 for(int i=1;i<=n;++i){ 63 if(t>=c[i]) ans++; 64 else break; 65 t-=c[i]; 66 } 67 cout<<ans<<endl; 68 return 0; 69 }

【问题描述】 小 W 拥有一个国家,现在他希望建立一支军队来保护他的国家。他选中了 N 个女孩和 M 个男孩希望招募他们成为他的士兵。在没有任何先决条件的情况下,他招募一个士兵需要花费 10000RMB。现在小 W 可以利用这些人之间的关系来减少他的花费。如果女孩 X 和男孩 Y 存在有一个关系值 D(两人之间可能有多个关系值),而且她们之中有一个人被招募了。那么小 W 可以在招募另一个人的时候减少 D 的花费(实际 10000-D 的费用)。 现在给你这些男孩女孩之间的关系,希望你告诉小 W 告诉他招募所有人的最少花费。注意:招募某一个人时,只能利用一个关系。 【输入格式】 输入文件 conscription.in 中文件第一行包含三个整数 N,M,R。表示 N 个女孩,M 个男孩与 R 条关系。 接下来 R 行,每行包含三个整数 Xi,Yi 和 Di,表示女孩 Xi 和男孩 Yi 有 Di 的关系。 【输出格式】 conscription.out 中只有一行一个数为最小费用。 【输入输出样例】 conscription.in 5 5 8 4 3 6831 1 3 4583 0 0 6592 0 1 3063 3 3 4975 1 3 2049 4 2 2104 2 2 781 conscription.out 71071 【数据规模】 100%的数据:1<=N, M<=100000,0<=R<=200,000,0 <di< 10000
tag:最小生成树
思路:kruscal求最小生成树,稍作处理得出答案。可以用10000*人数再减去所有生成树的边权,也可以像我这样最后查祖先数。
1 #include<cstdio> 2 #include<algorithm> 3 #include<iostream> 4 #include<cmath> 5 #define maxn 100010 6 using namespace std; 7 long long ans; 8 int cnt,fa[maxn<<2],n,m,r,i,x,y,d,tot; 9 struct X{ 10 int u,v,w; 11 }e[maxn<<4]; 12 void add(int x,int y,int w) 13 { 14 e[++cnt].u=x; 15 e[cnt].v=y; 16 e[cnt].w=w; 17 } 18 int find(int x) 19 { 20 return x==fa[x]?x:fa[x]=find(fa[x]); 21 } 22 bool cmp(X a,X b) 23 { 24 return a.w<b.w; 25 } 26 int main() 27 { 28 //freopen("conscription.in","r",stdin); 29 //freopen("conscription.out","w",stdout); 30 scanf("%d%d%d",&n,&m,&r); 31 for(i=0;i<n+m;++i) fa[i]=i; 32 for(i=1;i<=r;++i){ 33 scanf("%d%d%d",&x,&y,&d); 34 add(x,y+n,10000-d); 35 add(y+n,x,10000-d); 36 } 37 sort(e+1,e+cnt+1,cmp); 38 for(i=1;i<=cnt;++i){ 39 int u=e[i].u,v=e[i].v,w=e[i].w; 40 int k1=find(u),k2=find(v); 41 if(k1!=k2){ 42 fa[k1]=k2; 43 ans+=w; 44 tot++; 45 } 46 if(tot+1==n+m) break; 47 } 48 cnt=0; 49 for(i=0;i<n+m;++i) if(fa[i]==i) cnt++; 50 ans+=cnt*10000; 51 cout<<ans<<endl; 52 return 0; 53 }
┈━═┈━═┈━═┈━═┈━═┈━═┈━═┈━═依旧华丽的分割线┈━═┈━═┈━═┈━═┈━═┈━═┈━═┈━═☆
芒果君:这次考试比上次高了10分啊233333333我居然进步了(不)。本来准备昨天下午写解题报告结果一直浪到现在OTZ考试的话还是比较缺乏经验,好多分都没拿到,而且还出了freopen里words写成book的爆0惨案QAQ 不过下次也要加油哦~
暑假第二次考试 冲刺Noip2017模拟赛2 解题报告——五十岚芒果酱
原文:http://www.cnblogs.com/12mango/p/7225703.html