http://codeforces.com/contest/219/problem/D
给一个n节点的有向无环图,要找一个这样的点:该点到其它n-1要逆转的道路最少,(边<u,v>,如果v要到u去,则要逆转该边方向)如果有多个这样的点,则升序输出所有
看了三篇博客,挺好的
http://blog.csdn.net/chl_3205/article/details/9284747
http://m.blog.csdn.net/qq_32570675/article/details/53691814 一遍dfs
http://blog.csdn.net/angon823/article/details/52316220
正向边权值为0,反向为1.
第一次dfs记录每个点到所有子树中需要改变的边的条数。 (自下向上推)(优化下只需求出根节点到所有的点需要改变的边的条数)
第二次dfs由父节点求子节点到所有点的需要改变的边的条数。(自上向下)
把边的方向化为权值,正向为1,逆向为0。
问题转化为找哪些点的在遍历全图后总权值最大。
这就是树形DP了,考虑每个节点,它可以从子树收获价值,也可以从父亲收获。所以dfs两遍,一边把子树的价值存到dps[i]里,再一遍把父亲的价值存到dpf[i]里。ans[i] = dps[i] + dpf[i]。这都是老套路了!
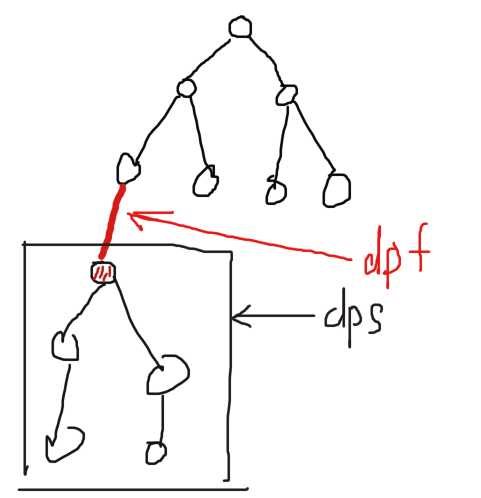
对于阴影那个点,第一遍dfs求出所有以下子节点(子树)对他的贡献,那么只有那根红线没有计算,第二遍dfs是计算父亲对他的贡献
代码一:
#include<bits/stdc++.h> using namespace std; typedef long long ll; #define MS(a) memset(a,0,sizeof(a)) #define MP make_pair #define PB push_back const int INF = 0x3f3f3f3f; const ll INFLL = 0x3f3f3f3f3f3f3f3fLL; inline ll read(){ ll x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } ////////////////////////////////////////////////////////////////////////// const int maxn = 2e5+10; int n,res,dp[maxn]; bool vis[maxn]; vector<pair<int,int> > g[maxn]; void dfs1(int u){ vis[u] = 1; for(int i=0; i<(int)g[u].size(); i++){ int v = g[u][i].first; if(vis[v]) continue; dfs1(v); res += g[u][i].second; } } void dfs2(int u){ vis[u] = 1; for(int i=0; i<(int)g[u].size(); i++){ int v = g[u][i].first, w = g[u][i].second; if(vis[v]) continue; if(w) dp[v] = dp[u]-1; else dp[v] = dp[u]+1; dfs2(v); } } int main(){ cin >> n; for(int i=1; i<n; i++){ int u,v; scanf("%d%d",&u,&v); g[u].push_back(MP(v,0)); g[v].push_back(MP(u,1)); } dfs1(1); dp[1] = res; MS(vis); dfs2(1); int mi = INF, last; for(int i=1; i<=n; i++) if(dp[i] <= mi) mi = dp[i]; cout << mi << endl; for(int i=1; i<=n; i++){ if(dp[i] == mi){ cout << i << " "; } } puts(""); return 0; }
代码二:
#include<bits/stdc++.h> using namespace std; typedef long long ll; #define MS(a) memset(a,0,sizeof(a)) #define MP make_pair #define PB push_back const int INF = 0x3f3f3f3f; const ll INFLL = 0x3f3f3f3f3f3f3f3fLL; inline ll read(){ ll x=0,f=1;char ch=getchar(); while(ch<‘0‘||ch>‘9‘){if(ch==‘-‘)f=-1;ch=getchar();} while(ch>=‘0‘&&ch<=‘9‘){x=x*10+ch-‘0‘;ch=getchar();} return x*f; } ////////////////////////////////////////////////////////////////////////// const int maxn = 1e6+10; int n,dps[maxn],dpf[maxn]; vector<pair<int,int> > g[maxn]; void dfs1(int u,int fa){ for(int i=0; i<(int)g[u].size(); i++){ int v = g[u][i].first, w = g[u][i].second; if(v == fa) continue; dfs1(v,u); dps[u] += w; dps[u] += dps[v]; } } void dfs2(int u,int fa){ for(int i=0; i<(int)g[u].size(); i++){ int v = g[u][i].first, w = g[u][i].second; if(v == fa) continue; dpf[v] = dpf[u]+dps[u]-dps[v]-w + (w?0:1); dfs2(v,u); } } int main(){ cin >> n; for(int i=1; i<n; i++){ int u,v; scanf("%d%d",&u,&v); g[u].push_back(MP(v,0)); g[v].push_back(MP(u,1)); } dfs1(1,-1); dfs2(1,-1); int mi = INF; for(int i=1; i<=n; i++) mi = min(mi,dps[i]+dpf[i]); cout << mi << endl; for(int i=1; i<=n; i++) if(dps[i]+dpf[i] == mi) cout << i << " "; puts(""); return 0; }
CodeForces 219D.Choosing Capital for Treeland (树形dp)
原文:http://www.cnblogs.com/yxg123123/p/7242481.html