红黑树是工程中最常用到的一种自平衡二叉排序树,其和AVL树类似,都是在进行插入、删除时通过一定的调整操作来维持相对稳定的树高,从而获得较好的查询性能。
1. 节点是红色或黑色。
2. 根节点是黑色。
3 每个叶节点(null节点)是黑色的。
4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
维护红黑树形状(树高)的,主要就是4、5两条性质,性质4决定了最长的路径莫过于红黑间隔的路径,性质5决定了最短的路径莫过于全黑路径,并且每条路径上的黑色节点数都相同(相当关键),二者共同决定了最长路径最多是最短路径的2倍。
插入的节点,应当是红色的,因为在叶节点插入红色节点不会违反性质5,而性质5恰恰是最难维护的。红黑树在插入操作后,需要维护性质2、4、5。
情况1:插入的是根节点。
原树是空树,此情况只会违反性质2,直接把此节点反转为黑色即可。
情况2:插入的节点的父节点是黑色。
此不会违反性质2和性质4,红黑树没有被破坏,什么也不做。
情况3:插入节点的父节点是红色且叔叔节点是红色。
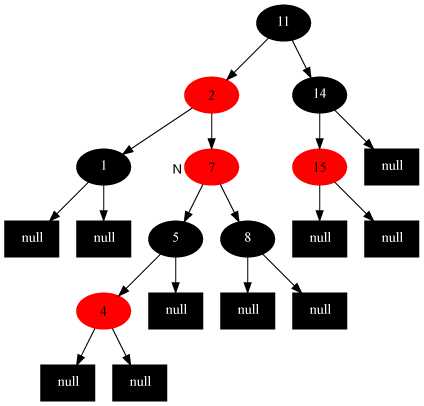
这种情况违反了性质4(新插入节点与父节点构成了连续的两个红节点),由于父节点与叔叔节点同为红色,故可将二者同置为黑色(此时违反了性质5),并将祖父节点置为红色(之前祖父节点一定为黑色)(遵守了性质5)。
N为插入节点
调整前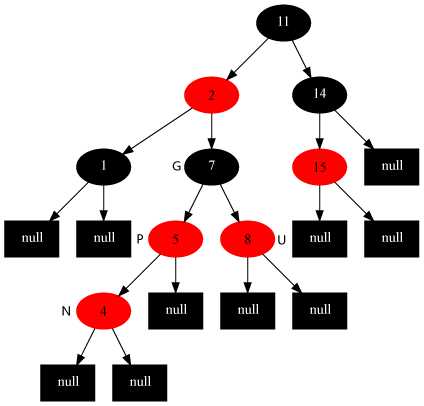
调整后
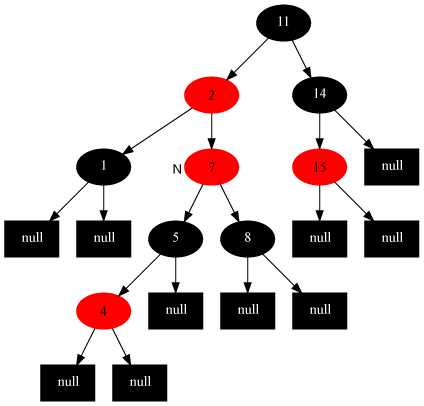
情况4:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的右子节点。
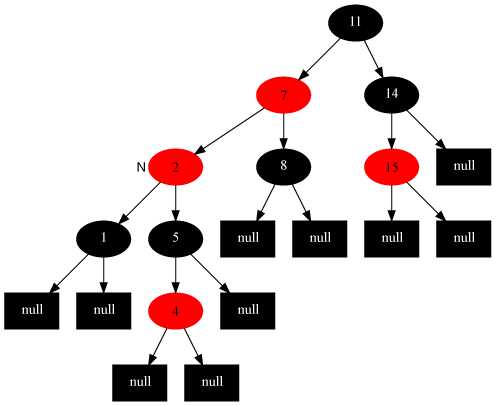
这种情况是最不好解决的,因为不管如何也无法通过一次变色或一次旋转完成调整,这种情况通常会与情况5结合使用,首先以插入节点的父节点为轴左旋。
调整前
调整后
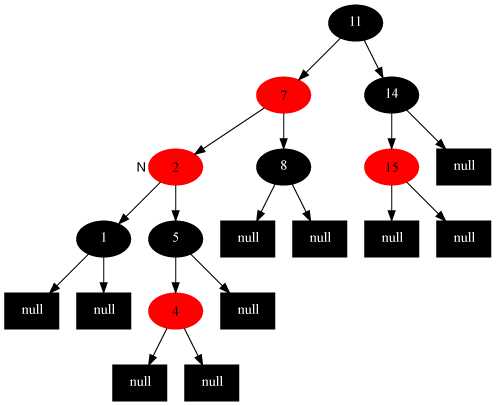
情况5:当前节点的父节点是红色,叔叔节点是黑色,当前节点是其父节点的左子节点。
接情况4,将插入节点的父节点置黑、祖父节点置红,以祖父节点为轴右旋。
调整前
调整后
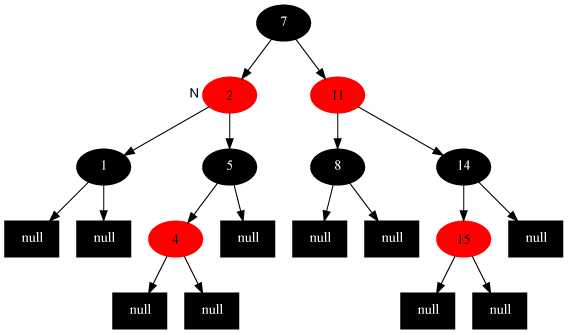
红黑树并不追求“完全平衡”——它只要求达到一种相对平衡(而AVL对平衡的要求就很严格,为之做出的努力也越多),降低了对旋转的要求,从而提高了性能。红黑树能够以O(log2 n) 的时间复杂度进行搜索、插入、删除操作。此外,由于它的设计,任何不平衡都会在三次旋转之内解决。当然,还有一些更好的,但实现起来更复杂的数据结构,能够做到一步旋转之内达到平衡,但红黑树能够给我们一个比较“便宜”的解决方案。
参考:http://www.imooc.com/article/11715
https://www.ibm.com/developerworks/cn/java/j-lo-tree/index.html
原文:http://www.cnblogs.com/holoyong/p/7247675.html