题意:求菲波那切数列的第n项。
分析:矩阵快速幂。
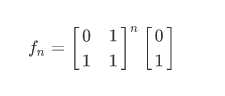
右边的矩阵为a0 ,a1,,,
然后求乘一次,就进一位,求第n项,就是矩阵的n次方后,再乘以b矩阵后的第一行的第一列。
#include <cstdio> #include <cstring> using namespace std; typedef long long ll; const int maxn = 101; const int maxm = 101; struct Matrix { int n,m; int a[maxn][maxm]; void clear() { n = m = 0; memset(a,0,sizeof(a)); } Matrix operator + (const Matrix &b) const { Matrix tmp; tmp.n = n; tmp.m = m; for(int i=0;i<n;++i) for(int j=0;j<m;++j) tmp.a[i][j] = a[i][j] + b.a[i][j]; return tmp; } Matrix operator - (const Matrix &b) const { Matrix tmp; tmp.n = n; tmp.m = m; for(int i=0;i<n;++i) for(int j=0;j<m;++j) tmp.a[i][j] = a[i][j] - b.a[i][j]; return tmp; } Matrix operator * (const Matrix & b) const { Matrix tmp; tmp.clear(); tmp.n = n; tmp.m = b.m; for(int i=0;i<n;++i) for(int j=0;j<b.m;++j) for(int k=0;k<m;++k) tmp.a[i][j] +=(a[i][k]*b.a[k][j])%10000; return tmp; } Matrix operator ^ (const int& k) const { Matrix tmp,t = *this; int p = k; tmp.clear(); tmp.m = tmp.n = this->n; for(int i=0;i<n;++i) tmp.a[i][i] = 1; while(p) { if(p&1) tmp = tmp*t; p>>=1; t = t*t; } return tmp; } }; int main(int argc, char const *argv[]) { int n; while(true) { scanf("%d",&n); if(n==-1) break; Matrix f; f.clear(); f.n = f.m = 2; f.a[0][0] = 0; f.a[0][1] = 1; f.a[1][0] = 1; f.a[1][1] = 1; f = f^n; Matrix x; x.clear(); x.n = 2; x.m = 1; x.a[0][0] = 0; x.a[1][0] = 1; f = f*x; printf("%d\n", f.a[0][0]); } return 0; }
原文:http://www.cnblogs.com/TreeDream/p/7256009.html