一个简单的神经网络结构:
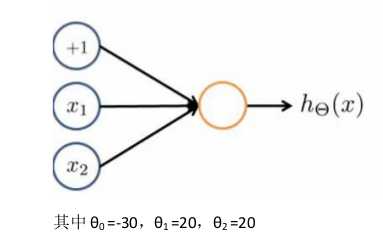
如图中如果 x1 x2 ∈{0,1}
y1 = x1 && x2 那么我们的输出函数hΘx = g (-30 + 20x1+20x2)
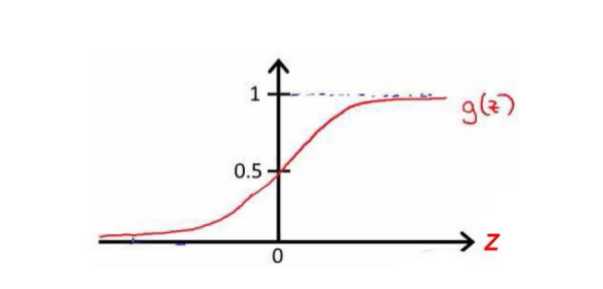
我们知道 g(x)的图像是
| x1 | x2 | hΘ(x) |
| 0 | 0 | g(-30)≈0 |
| 0 | 1 | g(-10)≈0 |
| 1 | 0 | g(-10)≈0 |
| 1 | 1 | g(10)≈1 |
所以我们有hΘ(x) ≈x1 & x2
这就是一个AND函数,同理,我们可以写一个OR函数的模型:

我们有hΘ(x) ≈x1 | x2
我们可以利用这些类似的神经元足额和起来成为更加复杂的运算,例如如果我们想要实现一个XNOR。
首先,构造一个能表达(Nx1)AND(Nx2)部分的神经元,然后将他们组合起来:
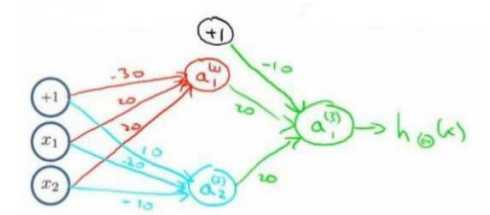
输入层 隐藏层 输出层
这块有点像数字电路与逻辑设计上的组合电路?)不过我们可以看出通过神经网络我们可通过对简单非线性函数的叠加组合。
对样本集{ (x1,y1) ...(xn,yn)}
L = total no of layers in network
sl = no of units
一元分类:y = 0,1 : SL = 1 k = 1
多元分类:SL = k hΘ(x)∈Rk(k≥3)
原文:http://www.cnblogs.com/KID-XiaoYuan/p/7271358.html