A:读懂题,乘一下判断大小就行了

#include<bits/stdc++.h> using namespace std; int main() { int s, v1, v2, t1, t2; scanf("%d%d%d%d%d", &s, &v1, &v2, &t1, &t2); int ans1 = v1 * s + t1 * 2, ans2 = v2 * s + t2 * 2; if(ans1 == ans2) puts("Friendship"); else if(ans1 < ans2) puts("First"); else puts("Second"); return 0; }
B:又是桶。。。cf怎么这么喜欢桶,当然把最小的位换成9是最好的,那么10个数字开10个桶,暴力删除每位改成9就行了,只是while要放在前面枚举pos

#include<bits/stdc++.h> using namespace std; int tot[10], sum, ans; char s[1000010]; int main() { int k; scanf("%d%s", &k, s); int len = strlen(s); for(int i = 0; i < len; ++i) ++tot[s[i] - ‘0‘], sum += s[i] - ‘0‘; int pos = 0; while(sum < k) { while(tot[pos] == 0) ++pos; sum += 9 - pos; --tot[pos]; ++ans; } printf("%d\n", ans); return 0; }
C:很明显不能暴力每次把所有星星+1,这是做不到的,但是看见c很小,那么我们预处理出c+1种情况就行了,可以用二维前缀和或二维bit,注意星星的位置可以重叠,考试的时候脑子坏了重新写了一遍,skip罚时爆炸,30min没了。。。
二维前缀和

#include<bits/stdc++.h> using namespace std; int a[11][110][110], mark[110][110]; vector<int> b[11][110][110]; int main() { int n, q, c; scanf("%d%d%d", &n, &q, &c); for(int i = 1; i <= n; ++i) { int x, y, s; scanf("%d%d%d", &x, &y, &s); mark[x][y] = 1; b[0][x][y].push_back(s); } for(int k = 0; k <= 10; ++k) for(int i = 1; i <= 101; ++i) for(int j = 1; j <= 101; ++j) { int delta = 0; if(k > 0) { for(int l = 0; l < b[k - 1][i][j].size(); ++l) { b[k][i][j].push_back((b[k - 1][i][j][l] + 1) % (c + 1)); delta += b[k][i][j][l]; } } else { for(int l = 0; l < b[k][i][j].size(); ++l) delta += b[k][i][j][l]; } a[k][i][j] = a[k][i][j - 1] + a[k][i - 1][j] - a[k][i - 1][j - 1] + delta; } for(int i = 1; i <= q; ++i) { int t, x1, y1, x2, y2; scanf("%d%d%d%d%d", &t, &x1, &y1, &x2, &y2); int sum = a[t % (c + 1)][x2][y2] - a[t % (c + 1)][x2][y1 - 1] - a[t % (c + 1)][x1 - 1][y2] + a[t % (c + 1)][x1 - 1][y1 - 1]; printf("%d\n", sum); } return 0; }
二维bit

#include<bits/stdc++.h> using namespace std; int a[11][110][110], mark[110][110]; int tree[11][110][110], x[1000010], y[1000010], s[100010][11]; int lowbit(int i) { return i & (-i); } void update(int k, int x, int y, int delta) { for(int i = x; i <= 101; i += lowbit(i)) for(int j = y; j <= 101; j += lowbit(j)) tree[k][i][j] += delta; } int query(int k, int x, int y) { int ret = 0; for(int i = x; i; i -= lowbit(i)) for(int j = y; j; j -= lowbit(j)) ret += tree[k][i][j]; return ret; } int main() { int n, q, c; scanf("%d%d%d", &n, &q, &c); for(int i = 1; i <= n; ++i) scanf("%d%d%d", &x[i], &y[i], &s[i][0]); for(int k = 0; k <= 10; ++k) for(int l = 1; l <= n; ++l) { if(k == 0) update(k, x[l], y[l], s[l][0]); else { s[l][k] = (s[l][k - 1] + 1) % (c + 1); update(k, x[l], y[l], s[l][k]); } } for(int i = 1; i <= q; ++i) { int t, x1, y1, x2, y2; scanf("%d%d%d%d%d", &t, &x1, &y1, &x2, &y2); int sum = query(t % (c + 1), x2, y2) - query(t % (c + 1), x2, y1 - 1) - query(t % (c + 1), x1 - 1, y2) + query(t % (c + 1), x1 - 1, y1 - 1); printf("%d\n", sum); } return 0; }
bit常数真是小,跑的跟前缀和一样快
D:怎么出原题,和7D有什么区别,直接拉板子。。。dp[i]表示第i位结束的串是多少palindrome,如果是回文,dp[i]=dp[i/2]+1,否则是0,判断回文用前后哈希,就是维护一个串正反的哈希,每次O(1)维护,然后枚举起点跑dp就行了。。。

#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N = 5010; char s[N]; int dp[N], ans[N]; int main() { scanf("%s", s + 1); int n = strlen(s + 1); for(int i = 1; i <= n; ++i) { memset(dp, 0, sizeof(dp)); ll p = 1, pre = 0, bak = 0; for(int j = i; j <= n; ++j) { pre = pre * 1234567ll + s[j]; bak = s[j] * p + bak; p *= 1234567ll; if(pre == bak) dp[j - i + 1] = dp[(j - i + 1) / 2] + 1; ++ans[dp[j - i + 1]]; } } for(int i = n; i; --i) ans[i] += ans[i + 1]; for(int i = 1; i <= n; ++i) printf("%d ", ans[i]); return 0; }
F:比较套路没想出来。。。zz。。。看见基环树,我们就要把环展开,具体方式是cycle存了环上每个点,最后push_back(cycle[0]),这样就首尾相接了,然后对于环上每个点维护max_d,挂在这个点下的最长链,pre_dia,从1->i这段环,包括环上点挂着的链的直径,pre_len,1->i这段环到1的最长路径,bak也一样
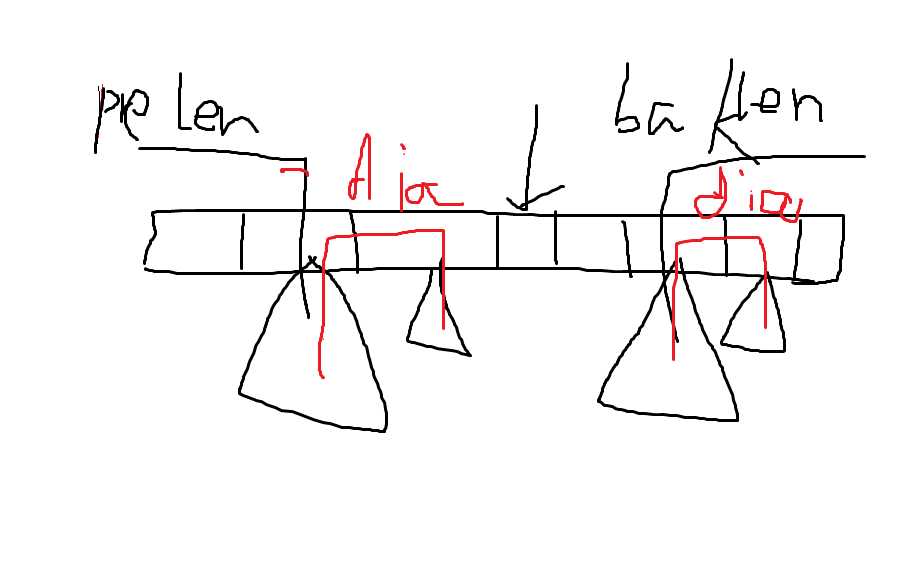
具体是这个样子的,然后枚举分割点,把环分割成两段后,mn=min(mn,max(pre_len+bak_len,max(pre_dia,bak_dia)),两段len相加构成了一条完全的链,两个dia分别是这两段的直径。
ans=max(ans,mn) ans先预处理不在环上的最长距离,就是子树内的直径,环上分割不影响这一段,所以和mn取max。注意最后push的cycle[0] max_d要取0,否则可能cycle在第一段和第二段都取了cycle[0],这样就不对了,但是后面一段的dia要加上max_d,因为两段dia是分别互不影响的,这个东西坑了我们长时间,又没办法对拍。。。

#include<bits/stdc++.h> using namespace std; typedef long long ll; const int N = 200010; inline int read() { int x = 0, f = 1; char c = getchar(); while(c < ‘0‘ || c > ‘9‘) { if(c == ‘-‘) f = -1; c = getchar(); } while(c >= ‘0‘ && c <= ‘9‘) { x = x * 10 + c - ‘0‘; c = getchar(); } return x * f; } struct edge { int to, w; edge(int to = 0, int w = 0) : to(to), w(w) {} }; ll ans = -1; int n, dfn_clock, tar; vector<edge> G[N]; vector<int> cycle; int dfn[N], mark[N]; ll w[N], pre_len[N], bak_len[N], pre_dia[N], bak_dia[N], max_d[N]; bool dfs(int u, int last) { if(dfn[u]) { tar = u; return true; } dfn[u] = ++dfn_clock; for(int i = 0; i < G[u].size(); ++i) { edge e = G[u][i]; if(e.to == last) continue; if(dfs(e.to, u)) { if(dfn[u] >= dfn[tar]) { cycle.push_back(u); mark[u] = 1; } return true; } } return false; } ll Dfs(int u, int last) { ll max_d = 0; for(int i = 0; i < G[u].size(); ++i) { edge e = G[u][i]; if(e.to == last || mark[e.to]) continue; ll dep = Dfs(e.to, u); ans = max(ans, dep + max_d + (ll)e.w); max_d = max(max_d, dep + (ll)e.w); } return max_d; } int main() { n = read(); for(int i = 1; i <= n; ++i) { int u = read(), v = read(), w = read(); G[u].push_back(edge(v, w)); G[v].push_back(edge(u, w)); } dfs(1, 0); reverse(cycle.begin(), cycle.end()); cycle.push_back(cycle[0]); for(int i = 0; i < cycle.size() - 1; ++i) { int u = cycle[i], v = cycle[i + 1]; for(int j = 0; j < G[u].size(); ++j) { edge e = G[u][j]; if(e.to == v) { w[i] = e.w; break; } } max_d[i] = Dfs(u, 0); } max_d[cycle.size() - 1] = max_d[0]; ll cur_len = 0, cur_dia = max_d[0]; pre_len[0] = pre_dia[0] = max_d[0]; for(int i = 1; i < cycle.size(); ++i) { cur_len += w[i - 1]; cur_dia += w[i - 1]; pre_len[i] = max(pre_len[i - 1], cur_len + max_d[i]); pre_dia[i] = max(pre_dia[i - 1], cur_dia + max_d[i]); cur_dia = max(cur_dia, max_d[i]); } cur_len = 0; cur_dia = max_d[cycle.size() - 1]; bak_dia[cycle.size() - 1] = max_d[cycle.size() - 1]; for(int i = cycle.size() - 2; i >= 0; --i) { cur_len += w[i]; cur_dia += w[i]; bak_len[i] = max(bak_len[i + 1], cur_len + max_d[i]); bak_dia[i] = max(bak_dia[i + 1], cur_dia + max_d[i]); cur_dia = max(cur_dia, max_d[i]); } ll mn = 1000000000000000ll; for(int i = 0; i < cycle.size() - 1; ++i) { mn = min(mn, max(pre_len[i] + bak_len[i + 1], max(pre_dia[i], bak_dia[i + 1]))); // ans = min(ans, pre_len[i] + bak_len[i + 1]); } printf("%lld\n", max(ans, mn)); return 0; }
原文:http://www.cnblogs.com/19992147orz/p/7276861.html