Hnoi2007-Day1有一道题目 Park:给你一个 m * n 的矩阵,每个矩阵内有个
权值V(i,j) (可能为负数),要求找一条回路,使得每个点最多经过一次,并且经过
的点权值之和最大,想必大家印象深刻吧.
无聊的小 C 同学把这个问题稍微改了一下:要求找一条路径,使得每个点
最多经过一次,并且点权值之和最大,如果你跟小 C 一样无聊,就麻烦做一下
这个题目吧.
转载请注明原文地址:http://www.cnblogs.com/LadyLex/p/7326874.html
最近搞了一下插头DP的基础知识……这真的是一种很锻炼人的题型……
每一道题的状态都不一样,并且有不少的分类讨论,让插头DP十分锻炼思维的全面性和严谨性。
下面我们一起来学习插头DP的内容吧!
插头DP主要用来处理一系列基于连通性状态压缩的动态规划问题,处理的具体问题有很多种,并且一般数据规模较小。
由于棋盘有很特殊的结构,使得它可以与“连通性”有很强的联系,因此插头DP最常见的应用要数在棋盘模型上的应用了。
下面我们给出一道很简单的例题,并且由这道简单的例题构建出插头DP的基本解题思路,在状态确立,状态转移以及程序实现几个方面进行一一介绍.
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
首先,我们要了解插头DP中最重要的关键词:“插头”
---插头
在插头DP中,插头表示一种联通的状态,以棋盘为例,一个格子有一个向某方向的插头,就意味着这个格子在这个方向可以与外面相连(与插头那边的格子联通)。
值得注意的一点是,插头不是表示将要去某处的虚拟状态,而是表示已经到达某处的现实状态。
也就是说,如果有一个插头指向某个格子,那么这个格子已经和插头来源联通了,我们接下来要考虑的是从这个插头往哪里走。
这是很重要的一点理解,下面讨论的状态转移都是在此基础上展开的,请务必注意。
我们已经有了插头,自然要利用插头来状态转移。一般来说,我们从上往下,从左往右逐行逐格递推。
---逐格递推
我们考虑第i行的某一个格子:走向它的方案,可能由上一行的下插头转移而来,也可能是本行的右插头转移而来。
因此我们需要记录这些地方有没有插头,也就是利用状压的思想。我们记录的这个“有没有插头”的东西,就被我们称为轮廓线。字面意思,轮廓线就是记录了棋盘这一行与上一行交界的轮廓中插头的情况。轮廓线上方是已经决策完的格子,下方是未决策的。显然,对于本题的轮廓线,与它直接相连的格子有m个,插头有m+1个,我个人的习惯是给插头编号0~m。

·上图就是轮廓线的一种可能情况。
由于数据范围比较小,轮廓线的插头状态我们一般可以利用X进制压位来表示。
对于本题来说,题目的限制条件比较少,可以走多个回路,而不是像某些题一样只能走一个回路(走一个回路的时候要维护插头间的连通性,我们下文再讨论),因此我们直接记录,只要用二进制来表示某一位置有没有插头即可:设0表示没有插头,1表示有插头。(大概这是最简单的一种插头类型了......)
---行间转移
我们先考虑两行之间的转移:显然,第i行的下插头决定了第i+1行的格子有没有上插头,因此我们应该把这个信息传递到下一行。
在转移的时候,当前行插头0到插头m-1可能会给下一行带来贡献,而第m个插头一定为0(结合定义,想一下为什么)。
容易发现,当前行的0~m-1号插头会变成下一行初始的1~m号插头,因此我们可以直接利用位运算进行转移。
对于本题,只需要将上一行的某个状态左移一位(<<1,即*2)即可
行间的转移还是比较简单的,具体代码实现的话,下面是一种可以参考的方式
(这是我刚学插头DP时候用的一种比较蠢的打法,使用状态数组f[i][j][k]表示决策到第i行第j列,插头状态为k的方案数,后面使用Hash表的时候我们还有其他方式)
1 if(i<n)//bin[i]表示2的i次方 2 for(int j=0;j<bin[m];j++) 3 f[i+1][0][j<<1]=f[i][m][j];
下面我们考虑具体的逐格转移,这也是插头DP的核心某块所在。
对于本题来说,当我们决策到某个格子(x,y)时,假如它不是障碍格子,可能会出现如下三种情况:

情况1,这个格子没有上插头,也没有左插头,那么由于我们要遍历整张图,所以我们要新建插头,把这个格子与其他格子连起来,相应的,我们要把原来轮廓线对应位置的插头改为1.
情况2,这个位置有上插头,也有左插头。由于我们不要求只有一条回路,因此回路可以在这里结束。我们直接更新答案即可。
情况3,只有一个插头。那么这个插头可以向其他方向走:向下和向右均可以。所以我们修改一下轮廓线并更新对应状态的答案即可。
值得注意的是,如果一个格子是障碍格,那么当且仅当没有插头连向它是,这才是一个合法状态。因为根据我们刚才插头的定义:
“值得注意的一点是,插头不是表示将要去某处的虚拟状态,而是表示已经到达某处的现实状态。
也就是说,如果有一个插头指向某个格子,那么这个格子已经和插头来源联通了,我们接下来要考虑的是从这个插头往哪里走。”
所以,对应障碍格既不能连入插头,也不能连出插头。这一点需要特别注意。
本题的分类讨论还是相对简单的,在处理完上面的内容后我们只需要按照上面的思路代码实现即可。
(代码里状态转移很有意思……)
1 #include <cstdio> 2 #include <cstring> 3 using namespace std; 4 typedef long long LL; 5 int n,m,bin[20],mp[13][13]; 6 LL f[13][13][(1<<12)+10]; 7 inline void Execution(int x,int y) 8 { 9 int plug1=bin[y-1],plug2=bin[y]; 10 for(int j=0;j<bin[m+1];j++) 11 if(mp[x][y]) 12 { 13 f[x][y][j]+=f[x][y-1][j^plug1^plug2];//如果2个都有插头,异或后变成均没有,2个都没有就变成都有 14 if(((j>>(y-1))&1)==((j>>y)&1))continue;//有一个的话,既可以转弯,也可以直走 15 f[x][y][j]+=f[x][y-1][j];//最开始学打的代码很蠢...下面哈希表会好一些 16 } 17 else 18 if(!(j&plug1)&&!(j&plug2))f[x][y][j]=f[x][y-1][j]; 19 else f[x][y][j]=0; 20 } 21 int main() 22 { 23 int t;scanf("%d",&t); 24 bin[0]=1;for(int i=1;i<=15;i++)bin[i]=bin[i-1]<<1; 25 for(int u=1;u<=t;u++) 26 { 27 scanf("%d%d",&n,&m); 28 for(int i=1;i<=n;i++) 29 for(int j=1;j<=m;j++) 30 scanf("%d",&mp[i][j]); 31 memset(f,0,sizeof(f));f[0][m][0]=1; 32 for(int i=1;i<=n;i++) 33 { 34 for(int j=1;j<=m;j++)Execution(i,j); 35 if(i<n) 36 for(int j=0;j<bin[m];j++) 37 f[i+1][0][j<<1]=f[i][m][j]; 38 } 39 printf("Case %d: There are %lld ways to eat the trees.\n",u,f[n][m][0]); 40 } 41 }
通过刚才这道题,你应该已经对插头DP是什么,以及插头DP的基本概念与思想有了基本的了解。
那么下面,我们通过下一道题来强化分类讨论能力,以及学习对连通性的限制方法。
时间限制:10 s 内存限制:162 MB
Smith在P市的邮政局工作,他每天的工作是从邮局出发,到自己所管辖的所有邮筒取信件,然后带回邮局。
他所管辖的邮筒非常巧地排成了一个m*n的点阵(点阵中的间距都是相等的)。左上角的邮筒恰好在邮局的门口。
Smith是一个非常标新立异的人,他希望每天都能走不同的路线,但是同时,他又不希望路线的长度增加,他想知道他有多少条不同的路线可走。
你的程序需要根据给定的输入,给出符合题意的输出:
l 输入包括点阵的m和n的值;
l 你需要根据给出的输入,计算出Smith可选的不同路线的总条数;
输入文件postman.in只有一行。包括两个整数m, n(1 <= m <= 10, 1 <= n <= 20),表示了Smith管辖内的邮筒排成的点阵。
输出文件只有一行,只有一个整数,表示Smith可选的不同路线的条数。
2 2 说明:该输入表示,Smith管辖了2*2的一个邮筒点阵。
2

有了上一题的经验,不难看出,本题依然是一个在棋盘模型上解决的简单回路问题(简单回路是指起点和终点相同的简单路径)。
而我们要求的是能一遍遍历整个棋盘的简单回路个数。
可是,如果直接搬用上一题的做法,你会发现一些问题:

比如对于上图的情况,在上一题中这是一个合法解,但在本题中不是。那么我们就应该思考上题插头定义的片面性在哪里,并想出新的插头定义。
容易观察到,如果每个格子都在回路中的话,最后所有的格子应该都通过插头连接成了一个连通块。
因此我们还需要记录每行格子的连通情况.这时我们就要引入一种新的方法:最小表示法。这是一种用来标记连通性的方法。
具体的过程是:第一个非障碍格子以及与它连通的所有格子标记为1,然后再找第一个未标记的非障碍格子以及与它连通的格子标记为2,……重复这个过程,直到所有的格子都标记完毕.比如连通信息((1,2,5),(3,6),(4)),就可以表示为{1,1,2,3,1,2}
但是,在实际的代码实现中,这样的最小表示法有些冗余:如果某个格子没有下插头,那么它就不会对下一行的格子产生影响,这个状态就是多余的。
因此,我们转换优化的角度,用最小表示法来表示插头的联通性:如果这个插头存在,那么就标记这个插头对应的格子的连通标号,如果这个插头不存在,那么标记为0..
在这样优化后,不仅状态表示更加简单,而且状态总数将会大大减少.
接下来,我们用改进过的最小表示法,继续思考上面的问题:如何定义新的插头状态?
如果每个格子都在回路中的话,我们还可以得到,每个格子应该恰好有且仅有2个插头。
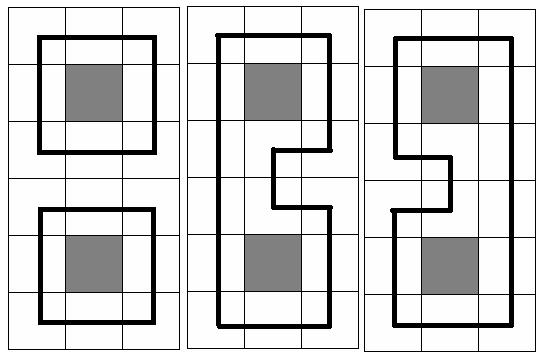
我们来看下面几张图片:

相信细心的你能够发现,轮廓线上方的路径是由若干条互不相交的路径构成的(这是肯定的,简单反证:如果最终相交就构不成回路了)。
更有趣的是,每条路径的两个端点恰好对应了轮廓线上的两个插头。
我们又知道,一条路径应该对应着一个连通块,因此这两个插头同属一个连通块,并且不与其他的连通块联通
并且,我们在状态转移的时候也不会改变这种性质:
上文的情况1对应着新增一条路径,插头为2;
情况2意味着把2条路径合为一条,联通块变为1个,插头还是2个;
情况3只有一个插头压根不会改变插头数量。
那么现在我们知道了,简单回路问题一定满足任何时候轮廓线上每一个连通分量恰好有2个插头。
互不相交……两个插头……展开你的联想,你能想到什么?
没错,这正是括号匹配!我们可以按照与括号匹配相似的方式,将轮廓线上每一条路径上中左边那个插头标记为左括号插头,右边那个插头标记为右括号插头。
由于插头之间不会交叉,那么左括号插头一定可以与右括号插头一一对应。
这样我们就可以解决上面的联通性问题:我们可以使用一种新的定义方式:3进制表示——0表示无插头,1表示左括号插头,2表示右括号插头记录下所有的轮廓线信息。
但是,值得注意的是,X进制的解码转码是较慢而且较麻烦的。
在空间允许的情况下,建议使用2k进制,并且加上Hash表去重。这样不仅可以减少状态,由于仍然可以使用位运算,运算速度相比之下也增加了不少。
下面,我们利用刚才新的插头定义方式来考虑本题的状态转移问题。
依然设当前转移到格子(x,y),设y-1号插头状态为p1,y号插头状态为p2。
情况1:p1==0&&p2==0.
这种状态和上一题的情况1是类似的,我们只需要新建一个新路径即可:下插头设为左括号插头,右插头设为右括号插头
情况2:p1==0&&p2!=0.
这种状态和上一题的状态3类似,我们依然可以选择“直走”和“转弯”两种策略
情况3:p1!=0&&p2==0.
这种状态和情况2类似,不再赘述。
情况4:p1==1&&p2==1.
这种状态把2个左括号插头相连,那么我们需要将右边那个左括号插头(p2)对应的右括号插头q2修改成左括号插头。
情况5:p1==1&&p2==2.
由于路径两两不相交,所以这种情况只能是自己和自己撞在了一起,即形成了回路。
由于只能有一条回路,因此只有在x==n&&y==m时,这种状态才是合法的,我们可以用它更新答案。



情况6:p1==2&&p2==1.
这种状态相当于把2条路径相连,并没有更改其他的插头
情况7:p1==2&&p2==2.
这种状态与情况4相似,这种状态把2个右括号插头相连,那么我们需要将左边那个右括号插头(p1)对应的左括号插头q1修改成右括号插头。
接下来我们只要代码实现上述过程即可。
但我们依然有一个很大的优化点:Hash表的使用。Hash表可以通过去重以及排除无用状态极大的加速插头DP的速度。
Hash表的打法不唯一,下面仅介绍我学习的打法(感谢stdafx学长)
与Hash表相关的主要内容有:
1.mod变量,为Hash表的大小和模数
2.size变量,存储Hash表大小;
3.hash数组,存储某个余数对应的编号
4.key数组,存储状态
5.val数组,存某个状态对应的方案数
在给出一个新状态时,我们在已有Hash表内搜索是否存在这一状态,如果有,那就修改这个状态对应的val值;如果没有,那就给他新建一个编号
具体的代码实现大概长这样:
1 struct Hash_Sheet 2 { 3 Data_Analysis val[mod];//本题(cogs1283)还要打高精度,所以比较毒瘤233 4 int key[mod],size,hash[mod]; 5 inline void Initialize() 6 { 7 memset(val,0,sizeof(val)),memset(key,-1,sizeof(key)); 8 size=0,memset(hash,0,sizeof(hash)); 9 } 10 inline void Newhash(int id,int v){hash[id]=++size,key[size]=v;} 11 Data_Analysis &operator [](const int State) 12 { 13 for(int i=State%mod;;i=(i+1==mod)?0:i+1) 14 { 15 if(!hash[i])Newhash(i,State); 16 if(key[hash[i]]==State)return val[hash[i]]; 17 } 18 } 19 }f[2];//每次清空Hash表,实现滚动
有了Hash表,我们再来考虑状态转移时的几个小细节:
我们状态转移的主要工作一般有三个:
1.查询某个插头对应的类型(对应下文Find)
2.查找与某个插头匹配的对应插头(对应下文Link)
3.修改状态中某个插头的类型(对应下文Set)
由于这三个操作很常用,所以我把他们写成了函数,方便调用。这三个操作的代码见下:
1 inline int Find(int State,int id){return (State>>((id-1)<<1))&3;} 2 inline void Set(int &State,int bit,int val){bit=(bit-1)<<1;State|=3<<bit,State^=3<<bit,State|=val<<bit;} 3 inline int Link(int State,int pos) 4 { 5 int cnt=0,Delta=(Find(State,pos)==1)?1:-1;//这个变量决定向左寻找匹配还是向右 6 for(int i=pos;i&&i<=m+1;i+=Delta) 7 { 8 int plug=Find(State,i); 9 if(plug==1)cnt++; 10 else if(plug==2)cnt--; 11 if(cnt==0)return i; 12 } 13 return -1; 14 }
有了上面这些操作,本题的全部代码实现已经水到渠成了:我们只需要把上面7种情况一一对应实现即可。代码见下:
(还有一个注意点,记得写高精度!)
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 #include <cmath> 5 using namespace std; 6 typedef long long LL; 7 const int cube=(int)1e9,mod=2601; 8 int n,m; 9 struct Data_Analysis 10 { 11 int bit[6]; 12 inline void Clear(){memset(bit,0,sizeof(bit));} 13 Data_Analysis(){Clear();} 14 inline void Set(int t){Clear();while(t)bit[++bit[0]]=t%cube,t/=cube;} 15 inline int &operator [](int x){return bit[x];} 16 inline void Print() 17 { 18 printf("%d",bit[bit[0]]); 19 for(int i=bit[0]-1;i>0;i--)printf("%09d",bit[i]); 20 printf("\n"); 21 } 22 inline Data_Analysis operator + (Data_Analysis b) 23 { 24 Data_Analysis c;c.Clear(); 25 c[0]=max(bit[0],b[0])+1; 26 for(int i=1;i<=c[0];i++) 27 c[i]+=bit[i]+b[i],c[i+1]+=c[i]/cube,c[i]%=cube; 28 while(!c[c[0]])c[0]--; 29 return c; 30 } 31 inline void operator += (Data_Analysis b){*this=*this+b;} 32 inline void operator = (int x){Set(x);} 33 }Ans; 34 struct Hash_Sheet 35 { 36 Data_Analysis val[mod]; 37 int key[mod],size,hash[mod]; 38 inline void Initialize() 39 { 40 memset(val,0,sizeof(val)),memset(key,-1,sizeof(key)); 41 size=0,memset(hash,0,sizeof(hash)); 42 } 43 inline void Newhash(int id,int v){hash[id]=++size,key[size]=v;} 44 Data_Analysis &operator [](const int State) 45 { 46 for(int i=State%mod;;i=(i+1==mod)?0:i+1) 47 { 48 if(!hash[i])Newhash(i,State); 49 if(key[hash[i]]==State)return val[hash[i]]; 50 } 51 } 52 }f[2]; 53 inline int Find(int State,int id){return (State>>((id-1)<<1))&3;} 54 inline void Set(int &State,int bit,int val){bit=(bit-1)<<1;State|=3<<bit,State^=3<<bit,State|=val<<bit;} 55 inline int Link(int State,int pos) 56 { 57 int cnt=0,Delta=(Find(State,pos)==1)?1:-1; 58 for(int i=pos;i&&i<=m+1;i+=Delta) 59 { 60 int plug=Find(State,i); 61 if(plug==1)cnt++; 62 else if(plug==2)cnt--; 63 if(cnt==0)return i; 64 } 65 return -1; 66 } 67 inline void Execution(int x,int y) 68 { 69 int now=((x-1)*m+y)&1,last=now^1,tot=f[last].size; 70 f[now].Initialize(); 71 for(int i=1;i<=tot;i++) 72 { 73 int State=f[last].key[i]; 74 Data_Analysis Val=f[last].val[i]; 75 int plug1=Find(State,y),plug2=Find(State,y+1); 76 if(Link(State,y)==-1||Link(State,y+1)==-1)continue; 77 if(!plug1&&!plug2){if(x!=n&&y!=m)Set(State,y,1),Set(State,y+1,2),f[now][State]+=Val;} 78 else if(plug1&&!plug2) 79 { 80 if(x!=n)f[now][State]+=Val; 81 if(y!=m)Set(State,y,0),Set(State,y+1,plug1),f[now][State]+=Val; 82 } 83 else if(!plug1&&plug2) 84 { 85 if(y!=m)f[now][State]+=Val; 86 if(x!=n)Set(State,y,plug2),Set(State,y+1,0),f[now][State]+=Val; 87 } 88 else if(plug1==1&&plug2==1) 89 Set(State,Link(State,y+1),1),Set(State,y,0),Set(State,y+1,0),f[now][State]+=Val; 90 else if(plug1==1&&plug2==2){if(x==n&&y==m)Ans+=Val;} 91 else if(plug1==2&&plug2==1)Set(State,y,0),Set(State,y+1,0),f[now][State]+=Val; 92 else if(plug1==2&&plug2==2) 93 Set(State,Link(State,y),2),Set(State,y,0),Set(State,y+1,0),f[now][State]+=Val; 94 } 95 } 96 int main() 97 { 98 scanf("%d%d",&n,&m); 99 if(n==1||m==1){printf("1\n");return 0;} 100 if(m>n)swap(n,m); 101 f[0].Initialize();f[0][0]=1; 102 for(int i=1;i<=n;i++) 103 { 104 for(int j=1;j<=m;j++)Execution(i,j); 105 if(i!=n) 106 { 107 int now=(i*m)&1,tot=f[now].size; 108 for(int j=1;j<=tot;j++) 109 f[now].key[j]<<=2; 110 } 111 } 112 Ans+=Ans;Ans.Print(); 113 }
通过这道题的历练,相信你对插头DP的插头定义,最小表示法,以及状态优化的方法有了一定的了解。
尤其需要培养的是插头定义的“手感”,插头定义绝对是你解题的关键。
接下来,我们把目光转移到“简单路径”上来。通过下面这道例题,相信会对这类简单路径&回路问题有更深的理解。
Hnoi2007-Day1有一道题目 Park:给你一个 m * n 的矩阵,每个矩阵内有个
权值V(i,j) (可能为负数),要求找一条回路,使得每个点最多经过一次,并且经过
的点权值之和最大,想必大家印象深刻吧.
无聊的小 C 同学把这个问题稍微改了一下:要求找一条路径,使得每个点
最多经过一次,并且点权值之和最大,如果你跟小 C 一样无聊,就麻烦做一下
这个题目吧.
第一行 m, n,接下来 m行每行 n 个数即V( i,j)
一个整数表示路径的最大权值之和.

1 inline bool check(int State) 2 { 3 int cnt=0,cnt1=0; 4 for(int i=1;i<=m+1;i++) 5 { 6 int plug=Find(State,i); 7 if(plug==3)cnt++; 8 else if(plug==1)cnt1++; 9 else if(plug==2)cnt1--; 10 } 11 return cnt>2||cnt1!=0; 12 }
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 const int N=110,M=10,mod=16631; 6 int n,m,ans,v[N][M]; 7 struct Hash_System 8 { 9 int key[mod],size,hash[mod],val[mod]; 10 inline void Initialize() 11 { 12 memset(key,-1,sizeof(key));memset(val,0xaf,sizeof(val)); 13 size=0;memset(hash,0,sizeof(hash)); 14 } 15 inline void Newhash(int id,int State){hash[id]=++size;key[size]=State;} 16 inline int &operator [] (const int State) 17 { 18 for(int i=State%mod;;i=(i+1==mod)?0:i+1) 19 { 20 if(!hash[i])Newhash(i,State); 21 if(key[hash[i]]==State)return val[hash[i]]; 22 } 23 } 24 }f[2]; 25 inline int max(int a,int b){return a>b?a:b;} 26 inline int Find(int State,int pos){return (State>>((pos-1)<<1))&3;} 27 inline void Set(int &State,int pos,int val){pos=(pos-1)<<1,State|=(3<<pos),State^=(3<<pos),State^=(val<<pos);} 28 inline int Link(int State,int pos) 29 { 30 int cnt=0,Delta=(Find(State,pos)==1)?1:-1; 31 for(int i=pos;i&&i<=m+1;i+=Delta) 32 { 33 int plug=Find(State,i); 34 if(plug==1)cnt++; 35 else if(plug==2)cnt--; 36 if(cnt==0)return i; 37 } 38 return -1; 39 } 40 inline bool check(int State) 41 { 42 int cnt=0,cnt1=0; 43 for(int i=1;i<=m+1;i++) 44 { 45 int plug=Find(State,i); 46 if(plug==3)cnt++; 47 else if(plug==1)cnt1++; 48 else if(plug==2)cnt1--; 49 } 50 return cnt>2||cnt1!=0; 51 } 52 inline void Execution(int x,int y) 53 { 54 int now=((x-1)*m+y)&1,last=now^1,tot=f[last].size; 55 f[now].Initialize(); 56 for(int i=1;i<=tot;i++) 57 { 58 int State=f[last].key[i],Val=f[last].val[i]; 59 if (check(State)||State>=(1<<((m+1)<<1)))continue; 60 int plug1=Find(State,y),plug2=Find(State,y+1); 61 int ideal=State;Set(ideal,y,0),Set(ideal,y+1,0);//ideal代表去掉y-1,y两个插头之后的轮廓线状态。 62 int empty1=ideal,empty2=ideal; 63 if(!plug1&&!plug2) 64 { 65 f[now][ideal]=max(f[now][ideal],Val); 66 if(x<n&&y<m)Set(State,y,1),Set(State,y+1,2),f[now][State]=max(f[now][State],Val+v[x][y]); 67 if(x<n)Set(empty1,y,3),f[now][empty1]=max(f[now][empty1],Val+v[x][y]); 68 if(y<m)Set(empty2,y+1,3),f[now][empty2]=max(f[now][empty2],Val+v[x][y]); 69 } 70 else if(plug1&&!plug2) 71 { 72 if(x<n)f[now][State]=max(f[now][State],Val+v[x][y]); 73 if(y<m)Set(empty1,y+1,plug1),f[now][empty1]=max(f[now][empty1],Val+v[x][y]); 74 if(plug1==3){if(!ideal)ans=max(ans,Val+v[x][y]);} 75 else Set(empty2,Link(State,y),3),f[now][empty2]=max(f[now][empty2],Val+v[x][y]); 76 } 77 else if(!plug1&&plug2) 78 { 79 if(y<m)f[now][State]=max(f[now][State],Val+v[x][y]); 80 if(x<n)Set(empty2,y,plug2),f[now][empty2]=max(f[now][empty2],Val+v[x][y]); 81 if(plug2==3){if(!ideal)ans=max(ans,Val+v[x][y]);} 82 else Set(empty1,Link(State,y+1),3),f[now][empty1]=max(f[now][empty1],Val+v[x][y]); 83 } 84 else if(plug1==1&&plug2==1)Set(empty1,Link(State,y+1),1),f[now][empty1]=max(f[now][empty1],Val+v[x][y]); 85 else if(plug1==1&&plug2==2)continue; 86 else if(plug1==2&&plug2==1)f[now][ideal]=max(f[now][ideal],Val+v[x][y]); 87 else if(plug1==2&&plug2==2)Set(empty2,Link(State,y),2),f[now][empty2]=max(f[now][empty2],Val+v[x][y]); 88 else if(plug1==3&&plug2==3){if(!ideal)ans=max(ans,Val+v[x][y]);} 89 else if(plug2==3)Set(empty1,Link(State,y),3),f[now][empty1]=max(f[now][empty1],Val+v[x][y]); 90 else if(plug1==3)Set(empty2,Link(State,y+1),3),f[now][empty2]=max(f[now][empty2],Val+v[x][y]); 91 } 92 } 93 int main() 94 { 95 scanf("%d%d",&n,&m); 96 for(register int i=1;i<=n;i++) 97 for(register int j=1;j<=m;j++) 98 scanf("%d",&v[i][j]),ans=max(ans,v[i][j]); 99 f[0].Initialize();f[0][0]=0; 100 for(register int i=1;i<=n;i++) 101 { 102 for(register int j=1;j<=m;j++)Execution(i,j); 103 if(i!=n) 104 for(int j=1,last=(i*m)&1,tot=f[last].size;j<=tot;j++) 105 f[last].key[j]<<=2; 106 } 107 printf("%d\n",ans); 108 }
lxhgww的小名叫“小L”,这是因为他总是很喜欢L型的东西。小L家的客厅是一个![]() 的矩形,现在他想用L型的地板来铺满整个客厅,客厅里有些位置有柱子,不能铺地板。现在小L想知道,用L型的地板铺满整个客厅有多少种不同的方案?
的矩形,现在他想用L型的地板来铺满整个客厅,客厅里有些位置有柱子,不能铺地板。现在小L想知道,用L型的地板铺满整个客厅有多少种不同的方案?
需要注意的是,如下图所示,L型地板的两端长度可以任意变化,但不能长度为0。铺设完成后,客厅里面所有没有柱子的地方都必须铺上地板,但同一个地方不能被铺多次。

输入的第一行包含两个整数,R和C,表示客厅的大小。
接着是R行,每行C个字符。’_’表示对应的位置是空的,必须铺地板;’*’表示对应的位置有柱子,不能铺地板。
输出一行,包含一个整数,表示铺满整个客厅的方案数。由于这个数可能很大,只需输出它除以20110520的余数。
R*C<=100
看到这道题,我们很容易发现上面几道题的所有插头定义方式都不在适用了。
因此,我们需要自行寻找到新的插头定义方式。
容易注意到,和上题的“路径”相比,本题的合法路径“L型地板”有一些特殊的地方:拐弯且仅拐弯一次。
这由于一条路径只有两种状态:拐弯过和没拐弯过,因此我们可以尝试着这样定义新的插头:
我们使用三进制,0代表没有插头,1代表没拐弯过的路径,2代表已经拐弯过的路径。
依然设当前转移到格子(x,y),设y-1号插头状态为p1,y号插头状态为p2。
那么会有下面的几种情况:
情况1:p1==0&&p2==0
这时我们有三种可选的策略:
①以当前位置为起点,从p1方向引出一条新的路径(把p1修改为1号插头)
②以当前位置为起点,从p2方向引出一条新的路径(把p2修改为1号插头)
③以当前位置为“L”型路径的转折点,向p1,p2两个方向均引出一个2号插头.
情况2:p1==0&&p2==1
由于p2节点还没有拐过弯,因此我们有2种可选的策略:
①继续直走,不拐弯,即上->下(把p1修改为1号插头,p2置0)
②选择拐弯,即上->右(把p2改为2号插头)
情况3:p1==1&&p2==0
这种情况和情况2类似,不再赘述。
情况4:p1==0&&p2==2
由于p2节点已经拐过弯,所以我们有如下的两种策略:
情况5:p1==2&&p2==0
这种情况与情况4类似,不再赘述。
情况6:p1==1&&p2==1
这种情况下,两块地板均没有拐过弯,因此我们可以在本格将这两块地板合并,形成一个合法的“L”型路径,并将本格看做他们的转折点。(把p1和p2都置为0)
至此,新插头定义的状态转移已经讨论完成。
不难发现,这种新的插头定义可以处理可能发生的所有可行情况。
我们只需要把他们转化为代码实现即可,具体见下:
1 #include <cstdio> 2 #include <cstring> 3 #include <algorithm> 4 using namespace std; 5 const int N=105,HASH=200097,mod=20110520; 6 int ans,n,m,last_x,last_y;char c[N][N];bool room[N][N]; 7 struct Hash_System 8 { 9 int val[HASH],key[HASH],hash[HASH],size; 10 inline void Initialize() 11 { 12 memset(val,0,sizeof(val)),memset(hash,0,sizeof(hash)); 13 memset(key,-1,sizeof(key)),size=0; 14 } 15 inline void Newhash(int id,int State){hash[id]=++size,key[size]=State;} 16 inline int &operator [] (const int State) 17 { 18 for(register int i=State%HASH;;i=(i+1==HASH)?0:i+1) 19 { 20 if(!hash[i])Newhash(i,State); 21 if(key[hash[i]]==State)return val[hash[i]]; 22 } 23 } 24 }f[2]; 25 inline int Find(int State,int pos){return (State>>((pos-1)<<1))&3;} 26 inline void Set(int &State,int pos,int val) 27 {pos=(pos-1)<<1,State|=(3<<pos),State^=(3<<pos),State^=(val<<pos);} 28 inline void Print(int State){for(int i=0;i<=m;i++)printf("%d",(State>>(i<<1))&3);} 29 inline void Execution(int x,int y) 30 { 31 register int now=((x-1)*m+y)&1,last=now^1,tot=f[last].size; 32 f[now].Initialize(); 33 for(register int i=1;i<=tot;i++) 34 { 35 int State=f[last].key[i],Val=f[last].val[i]; 36 int plug1=Find(State,y),plug2=Find(State,y+1); 37 if(room[x][y]) 38 { 39 if(!plug1&&!plug2) 40 { 41 if(room[x+1][y])Set(State,y,1),Set(State,y+1,0),f[now][State]=(f[now][State]+Val)%mod; 42 if(room[x][y+1])Set(State,y,0),Set(State,y+1,1),f[now][State]=(f[now][State]+Val)%mod; 43 if(room[x][y+1]&&room[x+1][y])Set(State,y,2),Set(State,y+1,2),f[now][State]=(f[now][State]+Val)%mod; 44 } 45 else if(!plug1&&plug2) 46 { 47 if(plug2==1) 48 { 49 if(room[x+1][y])Set(State,y,1),Set(State,y+1,0),f[now][State]=(f[now][State]+Val)%mod; 50 if(room[x][y+1])Set(State,y,0),Set(State,y+1,2),f[now][State]=(f[now][State]+Val)%mod; 51 } 52 else 53 { 54 Set(State,y,0),Set(State,y+1,0),f[now][State]=(f[now][State]+Val)%mod; 55 if(x==last_x&&y==last_y&&!State)ans=(ans+Val)%mod; 56 if(room[x+1][y])Set(State,y,2),Set(State,y+1,0),f[now][State]=(f[now][State]+Val)%mod; 57 } 58 } 59 else if(plug1&&!plug2) 60 { 61 if(plug1==1) 62 { 63 if(room[x][y+1])Set(State,y,0),Set(State,y+1,1),f[now][State]=(f[now][State]+Val)%mod; 64 if(room[x+1][y])Set(State,y,2),Set(State,y+1,0),f[now][State]=(f[now][State]+Val)%mod; 65 } 66 else 67 { 68 Set(State,y,0),Set(State,y+1,0),f[now][State]=(f[now][State]+Val)%mod; 69 if(x==last_x&&y==last_y&&!State)ans=(ans+Val)%mod; 70 if(room[x][y+1])Set(State,y,0),Set(State,y+1,2),f[now][State]=(f[now][State]+Val)%mod; 71 } 72 } 73 else if(plug1==1&&plug2==1) 74 { 75 Set(State,y,0),Set(State,y+1,0),f[now][State]=(f[now][State]+Val)%mod; 76 if(x==last_x&&y==last_y&&!State)ans=(ans+Val)%mod; 77 } 78 } 79 else if(!plug1&&!plug2)f[now][State]=(f[now][State]+Val)%mod; 80 } 81 } 82 int main() 83 { 84 scanf("%d%d",&n,&m); 85 for(register int i=1;i<=n;i++)scanf("%s",c[i]+1); 86 for(register int i=1;i<=n;i++) 87 for(register int j=1;j<=m;j++)room[i][j]=(c[i][j]==‘*‘)?0:1; 88 if(m>n) 89 { 90 for(register int i=1;i<=n;i++) 91 for(register int j=i+1;j<=m;j++) 92 swap(room[i][j],room[j][i]); 93 swap(n,m); 94 } 95 for(register int i=1;i<=n;i++) 96 for(register int j=1;j<=m;j++) 97 if(room[i][j])last_x=i,last_y=j; 98 f[0].Initialize();f[0][0]=1; 99 for(register int i=1;i<=n;i++) 100 { 101 for(register int j=1;j<=m;j++)Execution(i,j); 102 if(i!=n) 103 for(register int j=1,last=(i*m)&1,tot=f[last].size;j<=tot;j++) 104 f[last].key[j]<<=2; 105 } 106 printf("%d\n",ans); 107 }
面对一道之前没有见过的问题,我们通过寻找插头的新定义成功解决了该题。
相信你已经对插头定义有了初步的了解,接下来,一定要在做题时继续培养这种能力,这样才能百战不殆。
下面,再给出几道不是那么简单的题目,有兴趣的读者可以试着做一下:
BZOJ1187.[HNOI2007]神奇游乐园
BZOJ2595[Wc2008]游览计划
POJ3133Manhattan Wiring
POJ1739 Tony‘s Tour
上面讲解的4道题都是插头DP中比较基础的问题,但各自都体现出了不同的侧重点。
插头DP是一类很美妙的问题,当你看到自己辛苦想出、码出的分类讨论AC的时候,心中一定会有很大的成就感吧!
希望读完这篇博文的你能有所收获,对插头DP有更深刻的了解!
[入门向选讲] 插头DP:从零概念到入门 (例题:HDU1693 COGS1283 BZOJ2310 BZOJ2331)
原文:http://www.cnblogs.com/LadyLex/p/7326874.html