转载请注明出处:http://blog.csdn.net/u012860063
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1025
2 1 2 2 1 3 1 2 2 3 3 1
Case 1: My king, at most 1 road can be built. Case 2: My king, at most 2 roads can be built.
注意区分road和roads
思路:
/*假设存在一个序列d[1..9] = 2 1 5 3 6 4 8 9 7,可以看出来它的LIS长度为5。
下面一步一步试着找出它。
我们定义一个序列B,然后令 i = 1 to 9 逐个考察这个序列。
此外,我们用一个变量Len来记录现在最长算到多少了
首先,把d[1]有序地放到B里,令B[1] = 2,就是说当只有1一个数字2的时候,长度为1的LIS的最小末尾是2。这时Len=1
然后,把d[2]有序地放到B里,令B[1] = 1,就是说长度为1的LIS的最小末尾是1,d[1]=2已经没用了,很容易理解吧。这时Len=1
接着,d[3] = 5,d[3]>B[1],所以令B[1+1]=B[2]=d[3]=5,就是说长度为2的LIS的最小末尾是5,很容易理解吧。这时候B[1..2]
= 1, 5,Len=2
再来,d[4] = 3,它正好加在1,5之间,放在1的位置显然不合适,因为1小于3,长度为1的LIS最小末尾应该是1,这样很容易推知,长度为2的LIS最小末尾是3,于是可以把5淘汰掉,这时候B[1..2]
= 1, 3,Len = 2
继续,d[5] = 6,它在3后面,因为B[2] = 3, 而6在3后面,于是很容易可以推知B[3] = 6, 这时B[1..3]
= 1, 3, 6,还是很容易理解吧? Len = 3 了噢。
第6个, d[6] = 4,你看它在3和6之间,于是我们就可以把6替换掉,得到B[3] = 4。B[1..3] = 1,
3, 4, Len继续等于3
第7个, d[7] = 8,它很大,比4大,嗯。于是B[4] = 8。Len变成4了
第8个, d[8] = 9,得到B[5] = 9,嗯。Len继续增大,到5了。
最后一个, d[9] = 7,它在B[3] = 4和B[4] = 8之间,所以我们知道,最新的B[4] =7,B[1..5]
= 1, 3, 4, 7, 9,Len = 5。
于是我们知道了LIS的长度为5。
!!!!! 注意。这个1,3,4,7,9不是LIS,它只是存储的对应长度LIS的最小末尾。有了这个末尾,我们就可以一个一个地插入数据。虽然最后一个d[9]
= 7更新进去对于这组数据没有什么意义,但是如果后面再出现两个数字 8 和 9,那么就可以把8更新到d[5], 9更新到d[6],得出LIS的长度为6。
然后应该发现一件事情了:在B中插入数据是有序的,而且是进行替换而不需要挪动——也就是说,我们可以使用二分查找,将每一个数字的插入时间优化到O(logN)~~~~~于是算法的时间复杂度就降低到了O(NlogN)~
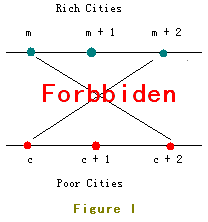
注意 把第一列的城市看成固定的,求出另一列数的最长递增序列
用ans[x]保存rich city的标号y,dp[i]存放的是长度为i的序列的末尾最小的那个ans[i]值
dp[]的长度就是最多的道路数目。
设辅助数组为dp[]。
可以知道最短len=1;此时dp[1]=ans[1],若第二个元素要大于第一个,把它加入dp[2],len++,
否则就更新dp[1],len不加,分析第三元素就可以推广到n个了,这样就降低分析问题的难度了。
如果第三个大于第二个元素就加入dp[3]中,如果小于第二个,直接更新dp[2]。
要判断left>len(left代表dp数组中更新元素的位置)这样2==2,不需要加。
如果小于第一个,更新dp[1],len=2>1,不需要加。
通过进一步分析:我们发现,dp数组中是递增的。它含有的元素的个数是当前上升子序列的个数(除0),
当有数据不是加入dp数组中,要更新前面的(用二分法找).而它不会影响结果,
因为dp数组中值(除0以外)的个数并没增加,要使len 增加,有两种可能:
1:后面有元素大于dp数组的最后一个元素就有(left>len)。
2:被另一个元素连续更新,且更新到left>len,意思就是说:选出另一元素它能比当前元素构造的上升子序列要多。
这样就能选出最长上升子序列了。
*/
代码如下:
#include <cstdio>
#include <cstring>
const int maxn = 500047;
int dp[maxn], ans[maxn], n;
int LIS()
{
dp[1] = ans[1]; //dp[i]用来存储长度为i时的最小值
int len = 1;
for (int i = 2; i <= n; i++)
{
int left = 1, right = len;
while (left <= right)//二分查找应该更新的元素
{
int m = (left + right)/2;
if (ans[i] > dp[m])
left = m + 1;
else
right = m - 1;
}
dp[left] = ans[i];
if (left > len)
len = left;
}
return len;
}
int main()
{
int x, y,k = 1;
while (~scanf("%d", &n))
{
for (int i = 0; i < n; i++)
{
scanf("%d%d", &x, &y);
ans[x] = y;
}
memset(dp, 0, sizeof(dp));
int len = LIS();
printf("Case %d:\n",k);
if(len==1)
printf("My king, at most 1 road can be built.");
else
printf("My king, at most %d roads can be built.",len);
printf("\n\n");
k++;
}
return 0;
}hdu1025 Constructing Roads In JGShining's Kingdom,布布扣,bubuko.com
hdu1025 Constructing Roads In JGShining's Kingdom
原文:http://blog.csdn.net/u012860063/article/details/32729409