题目链接:http://poj.org/problem?id=2195
Time Limit: 1000MS Memory Limit: 65536K
Description

Input
Output
Sample Input
2 2 .m H. 5 5 HH..m ..... ..... ..... mm..H 7 8 ...H.... ...H.... ...H.... mmmHmmmm ...H.... ...H.... ...H.... 0 0
Sample Output
2 10 28
转载请注明出处:優YoU http://blog.csdn.net/lyy289065406/article/details/6732762 大致题意: 给定一个N*M的地图,地图上有若干个man和house,且man与house的数量一致。man每移动一格需花费$1(即单位费用=单位距离),一间house只能入住一个man。现在要求所有的man都入住house,求最小费用。
构图: 把man作为一个顶点集合U,house作为另一个顶点集合V,把U中所有点到V中所有点addedge{from∈U,to∈V,cap=1,cost=两点间哈密顿距离},构成一个多源多汇的二分图。 构造一个超级源点s和超级汇点t:s与U中所有点相连,费用为0,容量为1;V中所有点与t相连,费用为0,容量为1。
这种构图思路很简单,我们建立起的二分图:
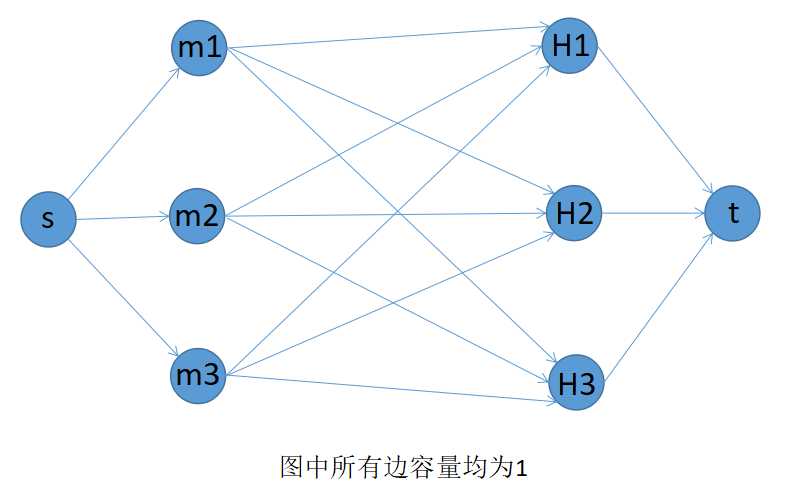
不难想象,maxflow必然等于the number of men(or the number of houses),在上图的例子中,即为3;
由于我们在所有man点与house点间建立的边容量为1,显然,最大流保证了:
①所有man都能到house里;
②一个man只进到一间house,一间house只有一个man;
就像在上图中,最大流的情况下,每个m[i]只能选一个H[j],而且i,j也不能重复;
这恰好就满足了题目所给的要求,然后,只要我们在m[i]到H[j]的边上加上cost=Hamiltonian_distance(m[i],H[j]),求出最小费用就是答案啦。
1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<vector> 5 #include<queue> 6 #define MAXN 203 7 #define INF 0x3f3f3f3f 8 using namespace std; 9 struct Edge{ 10 int u,v,c,f,a; 11 }; 12 struct MCMF 13 { 14 int s,t; 15 vector<Edge> E; 16 vector<int> G[MAXN]; 17 int vis[MAXN]; 18 int d[MAXN]; 19 int pre[MAXN]; 20 int aug[MAXN]; 21 void init(int l,int r) 22 { 23 for(int i=l;i<=r;i++) G[i].clear(); 24 E.clear(); 25 } 26 void addedge(int from,int to,int cap,int cost) 27 { 28 E.push_back((Edge){from,to,cap,0,cost}); 29 E.push_back((Edge){to,from,0,0,-cost}); 30 int m=E.size(); 31 G[from].push_back(m-2); 32 G[to].push_back(m-1); 33 } 34 bool SPFA(int s,int t,int &flow,int &cost) 35 { 36 memset(d,INF,sizeof(d)); 37 memset(vis,0,sizeof(vis)); 38 d[s]=0, vis[s]=1, pre[s]=0, aug[s]=INF; 39 queue<int> q; 40 q.push(s); 41 while(!q.empty()) 42 { 43 int now=q.front(); q.pop(); 44 vis[now]=0; 45 for(int i=0;i<G[now].size();i++) 46 { 47 Edge& e=E[G[now][i]]; 48 int nex=e.v; 49 if(e.c>e.f && d[nex]>d[now]+e.a) 50 { 51 d[nex]=d[now]+e.a; 52 pre[nex]=G[now][i]; 53 aug[nex]=min(aug[now],e.c-e.f); 54 if(!vis[nex]) 55 { 56 q.push(nex); 57 vis[nex]=1; 58 } 59 } 60 } 61 } 62 if(d[t]==INF) return 0; 63 flow+=aug[t]; 64 cost+=d[t]*aug[t]; 65 for(int i=t;i!=s;i=E[pre[i]].u) 66 { 67 E[pre[i]].f+=aug[t]; 68 E[pre[i]^1].f-=aug[t]; 69 } 70 return 1; 71 } 72 73 int mincost() 74 { 75 int flow=0,cost=0; 76 while(SPFA(s,t,flow,cost)); 77 return cost; 78 } 79 }mcmf; 80 81 char map[103][103]; 82 struct Node{int row,col;}; 83 int Hami_dist(Node a,Node b){return abs(a.row-b.row) + abs(a.col-b.col);} 84 85 int main() 86 { 87 int N,M;//N行,M列 88 while(scanf("%d%d",&N,&M) && N!=0) 89 { 90 vector<Node> men,houses; 91 for(int i=1;i<=N;i++) scanf("%s",map[i]+1); 92 for(int i=1;i<=N;i++) 93 { 94 for(int j=1;j<=M;j++) 95 { 96 if(map[i][j]==‘m‘) men.push_back((Node){i,j}); 97 if(map[i][j]==‘H‘) houses.push_back((Node){i,j}); 98 } 99 } 100 int n=men.size(); 101 mcmf.init(0,2*n+1); 102 mcmf.s=0, mcmf.t=2*n+1; 103 for(int i=0;i<n;i++) 104 { 105 mcmf.addedge(mcmf.s,i+1,1,0); 106 for(int j=0;j<n;j++) 107 { 108 if(i==0) mcmf.addedge(j+1+n,mcmf.t,1,0); 109 mcmf.addedge(i+1,j+1+n,1,Hami_dist(men[i],houses[j])); 110 } 111 } 112 printf("%d\n",mcmf.mincost()); 113 } 114 }
POJ 2195 - Going Home - [最小费用最大流][MCMF模板]
原文:http://www.cnblogs.com/dilthey/p/7417716.html