我的母亲柯蒂丽亚,是一个舞者。身披罗纱,一身异国装扮的她,来自灰狼的村子。
曾经在灰狼村子担任女侍的她,被认定在某晚犯下可怕的罪行之后,被赶出了村子。
一切的元凶,都要回到母亲犯下重罪的那一晚。
我不认为柯蒂丽亚有犯罪。
二十年前的混沌,一共有n块碎片。
这n块碎片曾经两两之间都有联系,可是很多联系都在时间的洪流中消失了。
现在,我只能确定其中m条联系的种类。
每条联系都是一条无向边,任意两块碎片之间至多有一条联系,没有联系会连接在同一块碎片的两端。
联系有两种。一种是冲突,用0表示;另一种是吻合,用1表示。
虽然已经过去了二十年,但是联系的种类是不会变的。
现在,我想要用这m条联系,去推断二十年前的n(n-1)/2条联系的种类。
如果我推理出所有联系的种类,那么我就可以将混沌言语化,证明柯蒂丽亚的清白。
在灰狼的村子,我得知了推理的唯一条件:
二十年前,对于任意三块互不相同的碎片,要么这三块碎片两两吻合,要么恰好有一对碎片互相吻合。
我想要知道,二十年前n块碎片两两之间的联系,可能有多少种。
你只要输出方案数模998244353之后的结果。如果已经确定的m条联系不符合上述条件,请输出0。
两种方案不同,当且仅当存在两块碎片,在一种方案中冲突,在另一种方案中吻合。也就是说,你要求的是有多少种可能的原图。
【输入描述】
第一行两个整数Test,T,Test表示测试点的编号,T表示数据的组数。保证T≤3。
接下来T组数据,每组数据第一行两个整数n,m,
接下来m行,每行三个整数u,v,t,表示第u块碎片和第v块碎片之间联系的种类为t。
【输出描述】
共T行,每行一个整数,表示方案数对998244353取模后的结果。
输入格式:
输出格式:
0 2 3 0 4 2 1 2 1 1 3 0
4 2
n <= 10^5
m <= 10^6
分析:考虑这样一个图: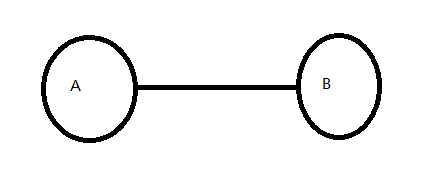 ,把一个连通块分成AB两部分,其中A和B两个不同的集合中每两个点都是吻合的,A集合的点到B集合的点之间每两个点都是冲突的.这样你任取三个点都是满足要求的.然后我们新加一个连通块:
,把一个连通块分成AB两部分,其中A和B两个不同的集合中每两个点都是吻合的,A集合的点到B集合的点之间每两个点都是冲突的.这样你任取三个点都是满足要求的.然后我们新加一个连通块: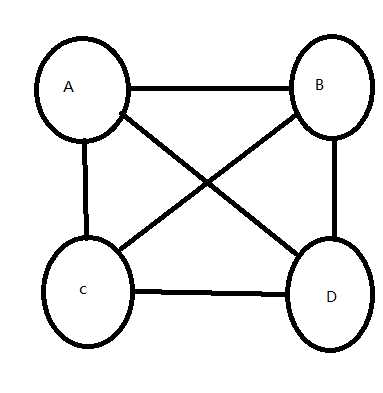 ,连线的代表都是冲突的,圆圈里的是吻合的,这是一种合法的方案,我们把CD交换一下,得到的又是一种新的方案,然后这两个连通块又可以合并成一个连通块.n个连通块有2*(n-1)条边连接,每两条边可以互换,这也就是说答案就是2^(cnt - 1),cnt为连通块个数。如果连通块退化成一个点也成立.
,连线的代表都是冲突的,圆圈里的是吻合的,这是一种合法的方案,我们把CD交换一下,得到的又是一种新的方案,然后这两个连通块又可以合并成一个连通块.n个连通块有2*(n-1)条边连接,每两条边可以互换,这也就是说答案就是2^(cnt - 1),cnt为连通块个数。如果连通块退化成一个点也成立.
关于如何求连通块个数:有向图可以用tarjan缩点,无向图可以用并查集.
考场上犯了几个脑残错误:1.flag没有清零 2.快速幂传递的参数传成了int,大数据直接爆掉QAQ,结果只有10分.
#include <cstdio> #include <cstring> #include <iostream> #include <algorithm> #include <cmath> using namespace std; const int mod = 998244353; int test, t, n, m, fa[300010]; bool flag = false; int find(int x) { if (x == fa[x]) return x; return fa[x] = find(fa[x]); } void hebing(int x, int y) { int fx = find(x), fy = find(y); if (fx != fy) fa[fy] = fx; } long long qpow(long long a, long long n) { long long result = 1; while (n) { if (n & 1) result = (result*a) % mod; a = (a*a) % mod; n >>= 1; } return result; } int main() { scanf("%d%d", &test, &t); while (t--) { flag = 0; scanf("%d%d", &n, &m); for (int i = 1; i <= 2 * n; i++) fa[i] = i; for (int i = 1; i <= m; i++) { int u, v, tt; scanf("%d%d%d", &u, &v, &tt); if (tt == 1) { if (find(u + n) == find(v) || find(u) == find(v + n)) flag = 1; else { hebing(u, v); hebing(u + n, v + n); } } else { if (find(u) == find(v) || find(u + n) == find(v + n)) flag = 1; else { hebing(u + n, v); hebing(u, v + n); } } } if (flag) printf("0\n"); else { int cnt = 0; for (int i = 1; i <= n; i++) if (fa[i] == i) cnt++; printf("%lld\n", qpow(2, cnt - 1)); } } return 0; }
原文:http://www.cnblogs.com/zbtrs/p/7420508.html