前言
以下内容是个人学习之后的感悟,如果有错误之处,还请多多包涵~
正则化
一、过拟合
过拟合是一种现象。当我们提高在训练数据上的表现时,在测试数据上反而下降,这就被称为过拟合,或过配。过拟合发生
的本质原因,是由于监督学习问题的不适定:在高中数学我们知道,从n个(线性无关)方程可以解n个变量,解n+1个变量就会解
不出。在监督学习中,当样本数远远少于特征数时,会发生过拟合现象。
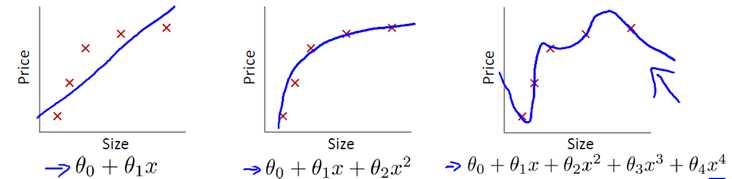
为了更直观地了解过拟合,请观察下面的图片。可以看到,左边是欠拟合,中间是正好拟合,右边是过拟合。经过对比,可以
看出过拟合能够符合所有的训练样本,但是结构弯弯曲曲,无法准确地测试数据。
针对过拟合现象一般有两个处理方法:
1、尽量减少特征量,将一些冗余的、信息量少的特征量舍弃。
2、使用正则化
二、正则化原理
使用正则化,其实只需要在代价函数后面加一个惩罚项即可。
Why? 为什么加一个惩罚项就可以了?
是的,看下面的例子。我们可以看到,二次多项式已经可以实现正确的拟合,采用四次多项式,就会产生过拟合。此时,我们
在代价函数的后面加上1000*(θ32,θ42)项,当代价函数最小化的时候,θ3≈0,θ4≈0,即假设函数变换到了二次多项式,避免了
过拟合。
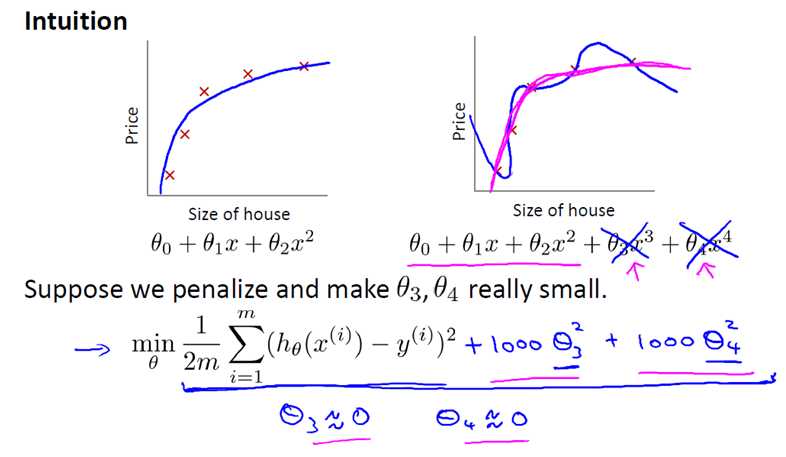
如果我们像惩罚 θ3 和 θ4 这样惩罚其它参数,那么我们往往可以得到一个相对较为简单的假设函数。实际上,这些参数的值
越小,通常对应于越光滑的函数,也就是更加简单的函数。因此 就不易发生过拟合的问题。按照惯例,我们没有去惩罚 θ0,因此
θ0 的值是大的。
三、线性回归正则化

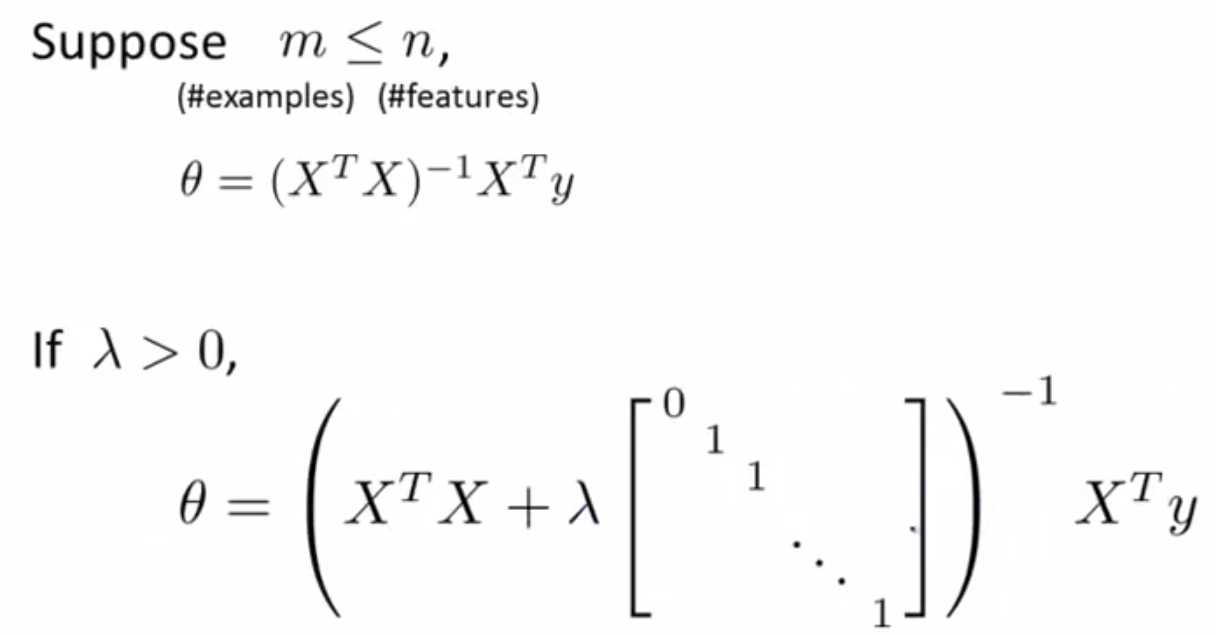
四、逻辑回归正则化
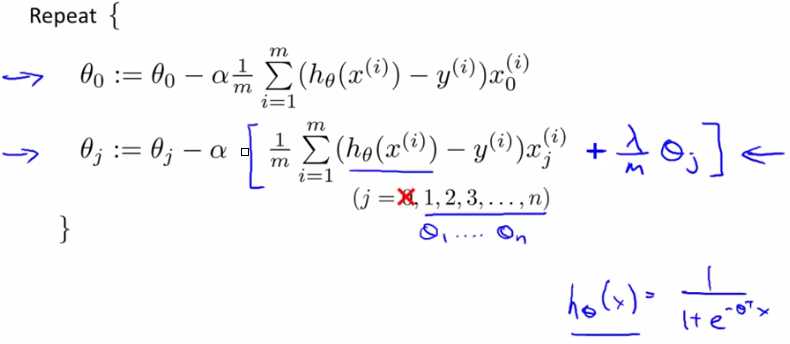
注1:λ的选取起到很关键的作用,之后会讲到相关的算法来实现自动取值λ。
注2:正则化不仅能够解决过拟现象,还能解决正规方程中奇异矩阵的问题。
以上是全部内容,如果有什么地方不对,请在下面留言,谢谢~
原文:http://www.cnblogs.com/steed/p/7436336.html