1、O(f(n))
学术界:O表示算法执行的上界,例如,归并算法的时间复杂度可以是O(nlogn),同时也是O(n^2)的
业界认为:O表示算法执行的最低上界,归并算法的时间复杂度是O(nlogn)
2、一个时间复杂度问题
一个字符串数组,将一每个字符串进行字母序排序,然后将字符串数组进行字典序排序的时间复杂度
n:数组长度 s:最大的字符串长度
O = s*nlogn (字符串数组排序)+ n* slogs(每个字符串)
3、数据规模 : 1S内可以处理的数据规模
O(N^2) :10^3~10^4
O(NLOGN) :10^6~10^7
O(n):10^7~10^8
4、空间复杂度:额外开通的数组规模
递归调用是牺牲空间的,系统需要将结果压入栈中,递归深度是多少就占多少空间
5、常见的模板时间复杂度
两个数交换:O(1)
1+2+....+N问题,是一重for循环: O(n)
字符串反转,第一个元素和最后一个元素, for(i = 0; i < n/2; i++):O(n)
选择排序,双重循环,i递增,j从i+1增:O(n^2)

双重循环:j变化是从1到一个常数:O(n)
二分查找,每次对半的查找,n/2的变化 经过多少次变为1:O(nlogn)

整数变为字符串:while里每次s+n%10,n = n/10: O(logn)
两重循环:n* logn

判断素数:

************* 有循环看循环的起始点,终止点和每次变化
6、验证算法时间复杂度:一层数据规模变化for,数据变化2倍,看运行时间变化
O(n):数据变化2倍,运行时间变化2倍
O(logn):随着数据规模的增加,运行时间基本不变
O(n^2):数据变化2倍,运行时间变化4倍
O(nlong):数据变化2倍,运行时间变化1倍多
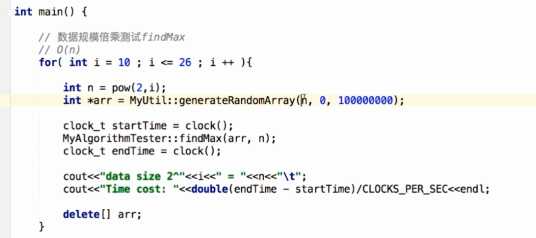
logn算法是最优的,数据规模越大,时间几乎没差别
7、递归算法时间复杂度:递归算法时间复杂度不一定是o(nlogn)
典型排序算法是递归算法:快速排序和归并排序 以及 二分查找的递归实现
7.1递归中只进行一次递归调用
1)递归中只进行一次的递归调用:

o(Logn):递归深度depth*每个递归函数中时间复杂度T = o(depth*T)
2) 1到n的和

3)优化了的求x^n次幂,(只能求n大于0的,计算机在处理基数时会进行舍位操作,所以判断是不是基数)

7.2 递归中多次调用递归,画出递归树
1)
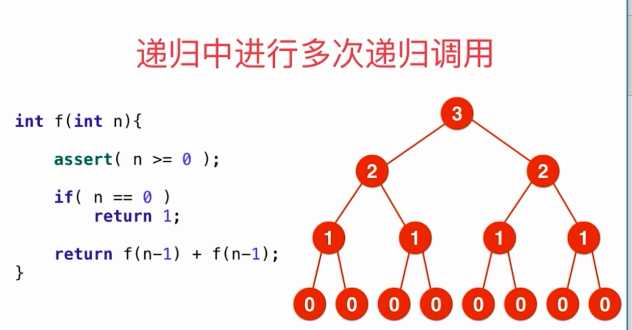
递归深度:2^0 + 2 ^1 + 2 ^2……+2 ^n = 2^(n+1) - 1 = O(2^n) 指数级的
指数的优化:通过剪支、动归为 多项式
搜索树
2)merge排序的时间复杂度O(nlogn)
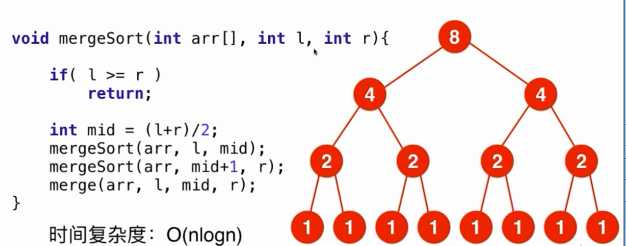
深度:logn
每个节点处理的数据规模是缩小的,每层n个节点,每个节点O(1)
7.3 主定理可查看更复杂的递归时间复杂度
以实现一个动态数组为例子:构造函数
7.4均分复杂度:
7.5防止复杂度震荡:删除数组的时候处理,当容量为当前的四分之一时,数组减小为size的二分之一。防止再次添加元素出现复杂度震荡。

原文:http://www.cnblogs.com/lingli-meng/p/7475907.html