package practice; import java.util.ArrayDeque; import java.util.Iterator; import java.util.Stack; public class TestMain { public static void main(String[] args) { Digraph a = new Digraph(13); a.addEdge(0, 1);a.addEdge(0, 5);/*a.addEdge(2, 3);*/a.addEdge(2, 0);a.addEdge(3, 2); /*a.addEdge(3, 5);*/a.addEdge(4, 3);/*a.addEdge(4, 2);*/a.addEdge(5, 4);a.addEdge(6, 0); a.addEdge(6, 4);a.addEdge(6, 9);a.addEdge(7, 6);/*a.addEdge(7, 8);*/a.addEdge(8, 7); a.addEdge(8, 9);a.addEdge(9, 10);a.addEdge(9, 11);a.addEdge(10, 12);a.addEdge(11, 4); a.addEdge(11, 12);/*a.addEdge(12, 9);*/ System.out.println(a); DirectedDFS dfsa = new DirectedDFS(a); //第一种方法检查环 System.out.println(dfsa.hasCycle()); System.out.println(); Digraph b = new Digraph(13); b.addEdge(0, 1);b.addEdge(0, 5);b.addEdge(2, 3);b.addEdge(2, 0);b.addEdge(3, 5); b.addEdge(5, 4);b.addEdge(6, 4);b.addEdge(6, 9);b.addEdge(7, 6);b.addEdge(8, 7); b.addEdge(9, 10);b.addEdge(9, 11);b.addEdge(9, 12);b.addEdge(11, 12);b.addEdge(0, 6); DirectedDFS dfsb = new DirectedDFS(b); //第一种方法检查环 System.out.println(dfsb.hasCycle()); for (Integer integer : dfsb.Topological()) { System.out.print(integer + " "); } } } /* * 有向图处理 */ class DirectedDFS { private boolean[] marked; private Digraph G; private Stack<Integer> cycle; private int []edgeTo; //轨迹 private boolean[] onStack; //当前搜索轨迹 private Stack<Integer> reversePost; //所有顶点的逆后续排列 /* * 在图处理类里初始化图 */ public DirectedDFS(Digraph G) { marked = new boolean[G.V()]; edgeTo = new int[G.V()]; this.G = G; DirectedCycle(); //检测环 DepthFirstOrder(); //拓扑排序 } /* * 深度优先搜索 */ private void dfs(int s) { marked[s] = true; for (int w : G.adj(s)) { if (!marked[w]) { edgeTo[w] = s; dfs(w); } } } /* * 广度优先搜索 */ private void bfs(int s) { ArrayDeque<Integer> deque = new ArrayDeque<Integer>(); deque.add(s); marked[s] = true; int c; while (!deque.isEmpty()) { c = deque.poll(); for (int w : G.adj(c)) { if (!marked[w]) { marked[w] = true; edgeTo[w] = c; deque.add(w); } } } } /* * 在G中找到s所有可达的顶点(可以用marked()检测) */ public void DFS(int s) { dfs(s); } /* * 在G中找到source中的所有顶点可到达的所有顶点 */ public void DFS(Iterable<Integer> sources) { for (Integer integer : sources) { dfs(integer); } } /* * v是可达的吗 */ public boolean marked(int v) { return marked[v]; } /* * 检测s到c的的路径 */ public void DFDPath(int s, int c) { for (int i = 0; i < marked.length; i++) { marked[i] = false; } dfs(s); System.out.print(c + "<-"); while (edgeTo[c] != s) { c = edgeTo[c]; System.out.print(c + "<-"); } c = edgeTo[c]; System.out.println(c); } /* * 检测s到c的的路径(最短) */ public void BFDPath(int s, int c) { for (int i = 0; i < marked.length; i++) { marked[i] = false; } bfs(s); System.out.print(c + "<-"); while (edgeTo[c] != s) { c = edgeTo[c]; System.out.print(c + "<-"); } c = edgeTo[c]; System.out.println(c); } /* * 检测该有向图是否有环 * 要标记当前路径,检查 将要检查到的(并已被标记过的点)是否在当前路径 */ private void DirectedCycle() { onStack = new boolean[G.V()]; //先将标记归零 for (int i = 0; i < marked.length; i++) { marked[i] = false; } //挨个搜索节点,标记过的节点就不搜了 for (int i = 0; i < G.V(); i++) { if (!marked[i]) DirectedCycleDfs(i); } } private void DirectedCycleDfs(int s) { onStack[s] = true; //onStack[v] = true 说明将v加入当前路径 marked[s] = true; for (int w : G.adj(s)) { if (this.hasCycle()) return; else if (!marked[w]) { edgeTo[w] = s; DirectedCycleDfs(w); } else if (onStack[w]) { //将这条路径保存到cycle cycle = new Stack<Integer>(); for (int x = s; x != w; x = edgeTo[x]) cycle.push(x); cycle.push(w); cycle.push(s); } } onStack[s] = false; //将要切换到另一条路径,将v从当前路径剔除 } //有环返回true无环返回false public boolean hasCycle() { return cycle != null;} //返回找到的环 public Iterable<Integer> cycle() { return cycle;} /* * 排出顶点的深度优先次序的深度优先搜索 * 拓扑排序 即被指向的一定在指向的后面 */ public void DepthFirstOrder() { reversePost = new Stack<Integer>(); for (int i = 0; i < marked.length; i++) { marked[i] = false; } for (int i = 0; i < G.V(); i++) { if (!marked[i]) dfo(i); } } private void dfo(int s) { marked[s] = true; for (int w : G.adj(s)) { if (!marked[w]) { dfo(w); } } reversePost.push(s); //可以保证被指向的肯定比指向的先进入栈,所以可以拓扑排序 } /* * 拓扑排序 */ public Iterable<Integer> Topological() { if (hasCycle()) { return null;} //有环则不能拓扑排序 return reversePost; } } /* * 有向图 */ class Digraph { private Bag<Integer>[] digraph; private int V; //点数 private int E; //边数 public Digraph(int V) { this.V = V; digraph = (Bag<Integer>[]) new Bag[V]; for (int i = 0; i < V; i++) { digraph[i] = new Bag<Integer>(); } } public int V() { return V;} public int E() { return E;} public void addEdge(int v, int w) { digraph[v].add(w); E++; } public Iterable<Integer> adj(int V) { return digraph[V]; } public Digraph reverse() { Digraph result = new Digraph(V); for (int i = 0; i < V; i++) { for (Integer integer : digraph[i]) { result.addEdge(i, integer); } } return result; } public String toString() { String s = V + " vertices, " + E + " edges\n"; for (int v = 0; v < V; v++) { s += v + ": "; for (Integer integer : this.adj(v)) { s += integer + " "; } s += "\n"; } return s; } } /* * 背包 */ class Bag<T> implements Iterable<T> { Node first; private class Node { T value; Node next; } public void add(T value) { Node oldfirst = first; first = new Node(); first.value = value; first.next = oldfirst; } @Override public Iterator<T> iterator() { return new BagIterator(); } private class BagIterator implements Iterator<T> { Node node = first; @Override public boolean hasNext() { return node != null; } @Override public T next() { T tempt = node.value; node = node.next; return tempt; } } }
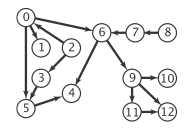
上面用到的有向图(Digraph b)
原文:http://www.cnblogs.com/zhangqi66/p/7484317.html