| Time Limit: 8000MS | Memory Limit: 30000K | |
| Total Submissions: 2622 | Accepted: 535 | |
| Case Time Limit: 3000MS | ||
Description
Input
Output
Sample Input
4 0.0 0 6.00 -0.001 3.125 4.747 4.747 0.47 5 3 7 0 4 -4.7 7 4.7 4 47 4 94
Sample Output
GOOD BAD BAD
Hint
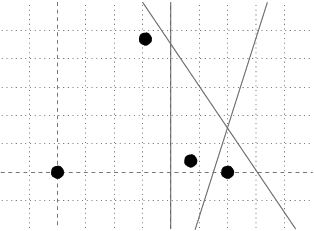
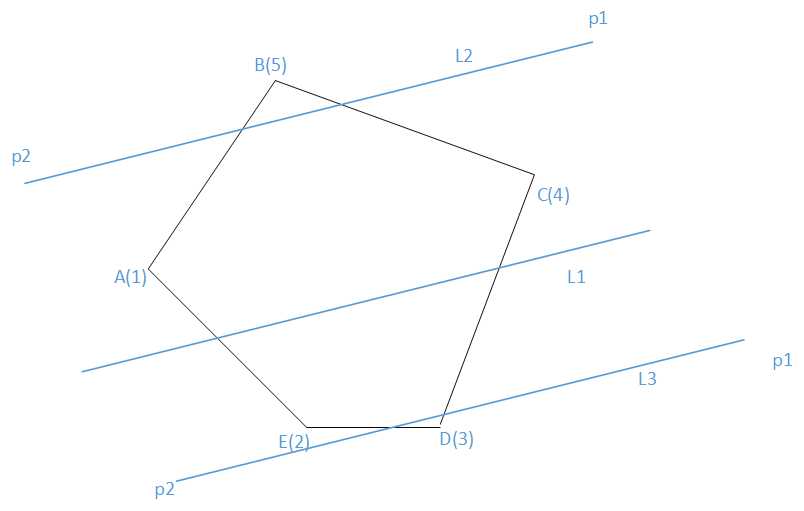
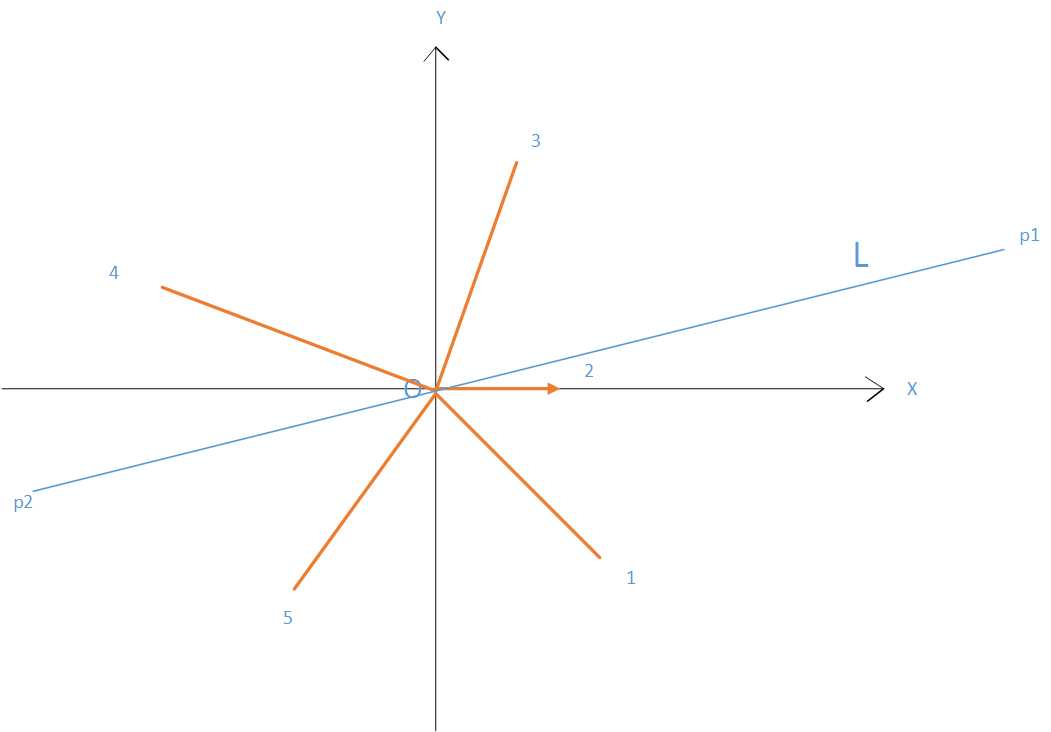
第一幅图中,向量AE,ED,DC,CB,BA的极角在 坐标系中变化是单调的,于是把他们都移到图二中来,都以O点为起点,按照极角大小排序并编号,凸包的算法因人而异,我现在用的凸包算法是以最左端的A点开始存储,并按照逆时针方向存储点的,那么AE向量最好标记为极角最小的向量,ED次之,以此类推,那么我们就得设定极角的变化范围为(-90,270],这样将所有的向量排好序,并标记好编号,譬如右图的1向量代表AE向量。。。现在又给出一条直线L1,如何得知L1和凸包相交呢?我们平移L1的向量形式,移到L1只割掉了凸包一个点的位置(一共两个位置),L2的方向为p1p2,L3的方向为p2p1,我们发现这两条向量如果都要逆时针转一个方向,分别转动到向量DC和向量BA的位置需要转动的角度是最小的,而向量DC和BA的端点D,B又恰恰是向量L3和L1所割掉的点那么如果线段DB和直线L1有交点,则L1一定和凸包存在交点的。这个规律放到图二来看,直线L的向量形式为p2p1,转到向量3是所转角度最小的,其反向的向量转到向量5转角度又是最小的,向量3与向量5都是可以通过二分查找找出来,找到向量之后在取其起始端点,判断这两个起始端点是否与直线相交。
AC代码:
#define _CRT_SECURE_NO_DEPRECATE #include<iostream> #include<stdio.h> #include<algorithm> #include<queue> #include<set> #include<vector> #include<cstring> #include<string> #include<functional> #include<cmath> #include<stack> using namespace std; const int N_MAX = 100000 + 5; #define INF 0x3f3f3f3f #define EPS 1e-10 #define equals(a,b) (fabs(a-b)<EPS) #define pi acos(-1.0) #define BOTTOM 0 #define LEFT 1 #define RIGHT 2 #define TOP 3 static const int COUNTER_CLOCKWISE = -1; static const int CLOCKWISE = 1; static const int ONLINE_BACK = 2; static const int ONLINE_FRONT = -2; static const int ON_SEGMENT = 0; double add(double a,double b) { if (abs(a + b) < EPS*(abs(a) + abs(b)))return 0; return a + b; } class point { public: double x, y; point(double x = 0, double y = 0) :x(x), y(y) {} point operator +(point p) { return point(x+p.x, y+p.y); } point operator -(point p) { return point(x - p.x,y - p.y); } point operator *(double a) { return point(a*x, a*y); } point operator /(double a) { return point(x / a, y / a); } double norm() { return x*x + y*y; } double abs() { return sqrt(norm()); } bool operator<(const point&p)const { return x != p.x ? x < p.x : y < p.y; } bool operator ==(const point&p)const { return x == p.x && y == p.y; } double dot(point p) { return x*p.x+y*p.y; } double det(point p) { return x*p.y- y*p.x; } }; struct Segment { point p1, p2; Segment(point p1 = point(), point p2 = point()) :p1(p1), p2(p2) {} }; typedef Segment line; typedef vector<point>Polygon; //????????????p0p1?????????p0p2??????????????? int ccw(point p0, point p1, point p2) { point a = p1 - p0; point b = p2 - p0; if (a.det(b) > EPS)return COUNTER_CLOCKWISE; if (a.det(b) < -EPS)return CLOCKWISE; if (a.dot(b) < -EPS)return ONLINE_BACK; if (a.norm() >= b.norm())return ON_SEGMENT;//!! return ONLINE_FRONT; } //????????????p1p2???p3p4???????????? bool intersect(point p1, point p2, point p3, point p4) { return (ccw(p1, p2, p3)*ccw(p1, p2, p4) < 0 && ccw(p3, p4, p1)*ccw(p3, p4, p2) < 0);//!!!!!!!!!!!!!!!!!!!!!!!!!!! } inline double normalize(double r) { if (r < -pi / 2.0 + EPS) r += pi * 2; return r; } double arg(const point& p) { return normalize(atan2(p.y, p.x)); } inline bool double_cmp(double a,double b) { return a + EPS < b; } //// typedef vector<point>Polygon; vector<point> convex_hull(point *ps, int N) { sort(ps, ps + N); int k = 0; // 凸包的顶点数 vector<point> qs(N * 2); // 构造中的凸包 // 构造凸包的下侧 for (int i = 0; i < N; ++i) { while (k > 1 && (qs[k - 1] - qs[k - 2]).det(ps[i] - qs[k - 1]) <= 0) --k; qs[k++] = ps[i]; } // 构造凸包的上侧 for (int i = N - 2, t = k; i >= 0; --i) { while (k > t && (qs[k - 1] - qs[k - 2]).det(ps[i] - qs[k - 1]) <= 0) --k; qs[k++] = ps[i]; } qs.resize(k - 1); return qs; } point s[N_MAX]; int n; double a[N_MAX];//记录凸包每条边行成的向量倾斜度 int main() { scanf("%d", &n); for (int i = 0; i < n; i++) { scanf("%lf%lf", &s[i].x, &s[i].y); } int N; Polygon con; if (n > 1) { con=convex_hull(s,n); N = con.size(); con.push_back(con[0]); } for (int i = 0; i <N; i++) { a[i] = arg(con[i + 1] - con[i]); } sort(a, a + N, double_cmp); point p1, p2; while (scanf("%lf%lf%lf%lf",&p1.x,&p1.y,&p2.x,&p2.y)!=EOF) { if (n < 2) { puts("GOOD"); continue; } int i = upper_bound(a, a + N, arg(p2 - p1), double_cmp) - a; int j = upper_bound(a, a + N, arg(p1 - p2), double_cmp) - a; puts((((p2 - p1).det(con[i] - p1) * (p2 - p1).det(con[j] - p1) > -EPS)) ? "GOOD" : "BAD"); } return 0; }
poj 1912 A highway and the seven dwarfs
原文:http://www.cnblogs.com/ZefengYao/p/7487823.html