排序二叉树对于我们寻找无序序列中的元素的效率有了大大的提高。查找的最差情况是树的高度。这里就有问题了,将无序数列转化为
二叉排序树的时候,树的结构是非常依赖无序序列的顺序,这样会出现极端的情况。
【如图1】:
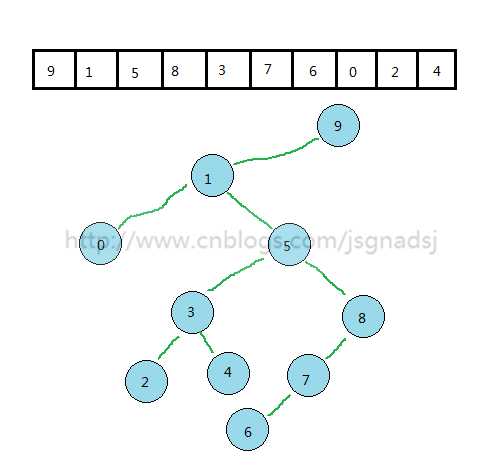
这样的一颗二叉排序树就是一颗比较极端的情况。我们在查找时候,效率依赖树的高度,所以不希望这样极端情况出现,而是希望元素比较均匀
的分布在根节点两端。
技术参考:fun4257.com/
问题提出:
能不能有一种方法,使得我们的二叉排序树不依赖无序序列的顺序,也能使得我们得到的二叉排序树是比较均匀的分布。
引入:
平衡二叉树(Self-Balancing Binary Search Tree 或 Height-Balanced Binary Search Tree),是一种特殊的二叉排序树,其中每一个结点的
左子树和右子树的高度差至多等于1.
这里的平衡从名字中可以看出,Height-Balanced是高度平衡。
它或者是一颗空树,或者是具有下列性质的二叉树:它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1.
若将二叉树上的结点的平衡因子BF(Balance Factor)定义为该节点的左子树的深度减去它的右子树的深度,则平衡二叉树上所有结点的平衡因子只
可能是-1、0、1。否则就不是平衡二叉树。
上图图1中,就不是平衡二叉树。
以图1来看看各个结点的平衡因子。
【如下图2】:
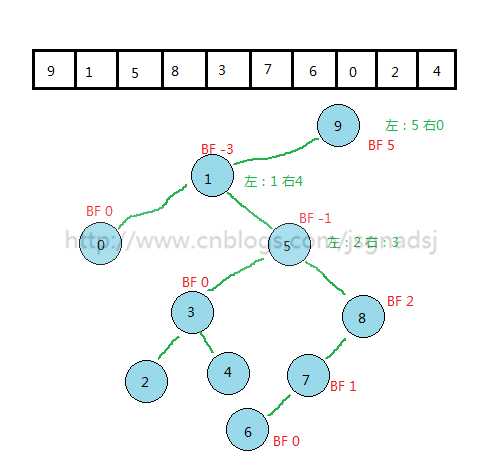
技术参考:fun1404.com
如何构成平衡二叉树?
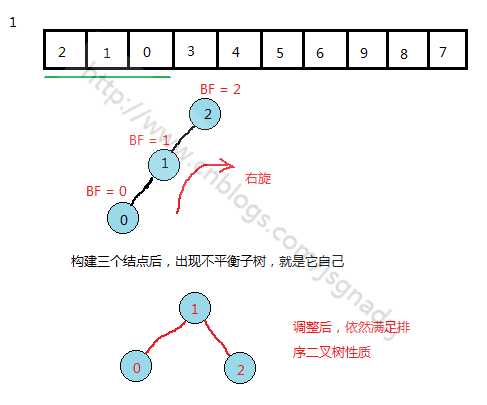
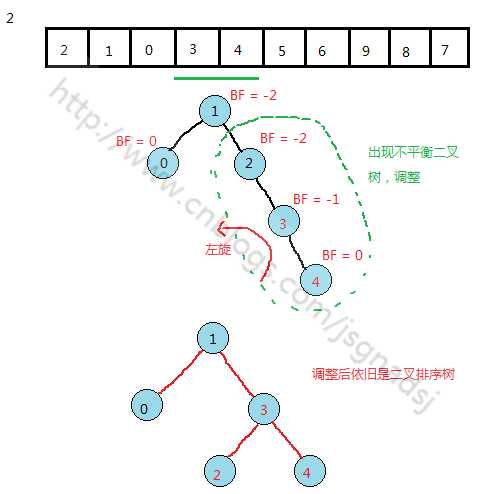
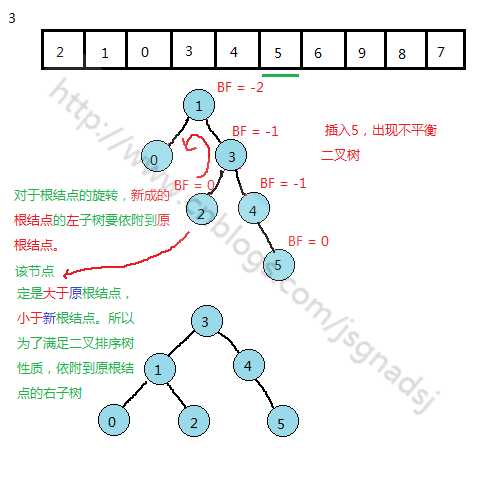
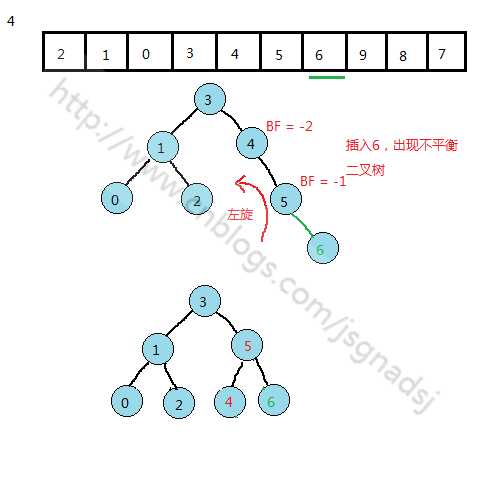
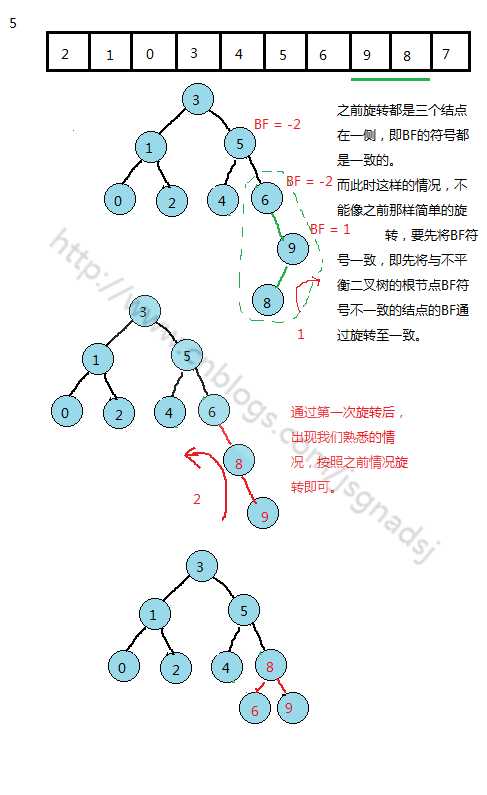
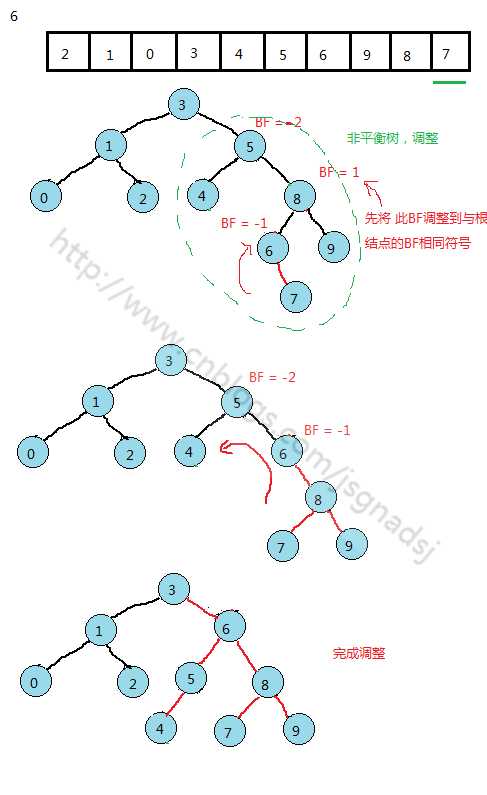
从转化为平衡二叉树的过程中可以提炼出转化的几个基本情况:
下图是在维基百科上摘录的:
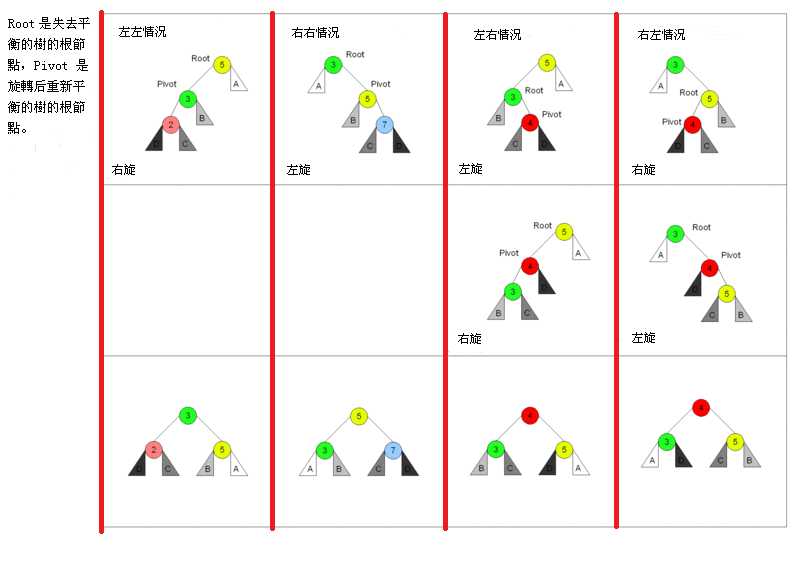
可以看出调整的操作分两大类,前两个是一组,后两个是一组,每组之间是对称的。
前两个是对应上图1 2 中情况,
后两个是对应上图5 6 中情况。
分别以其中一种旋转为例,另一种对应的旋转对称。
单次左旋:对应上图1(左左)中情况
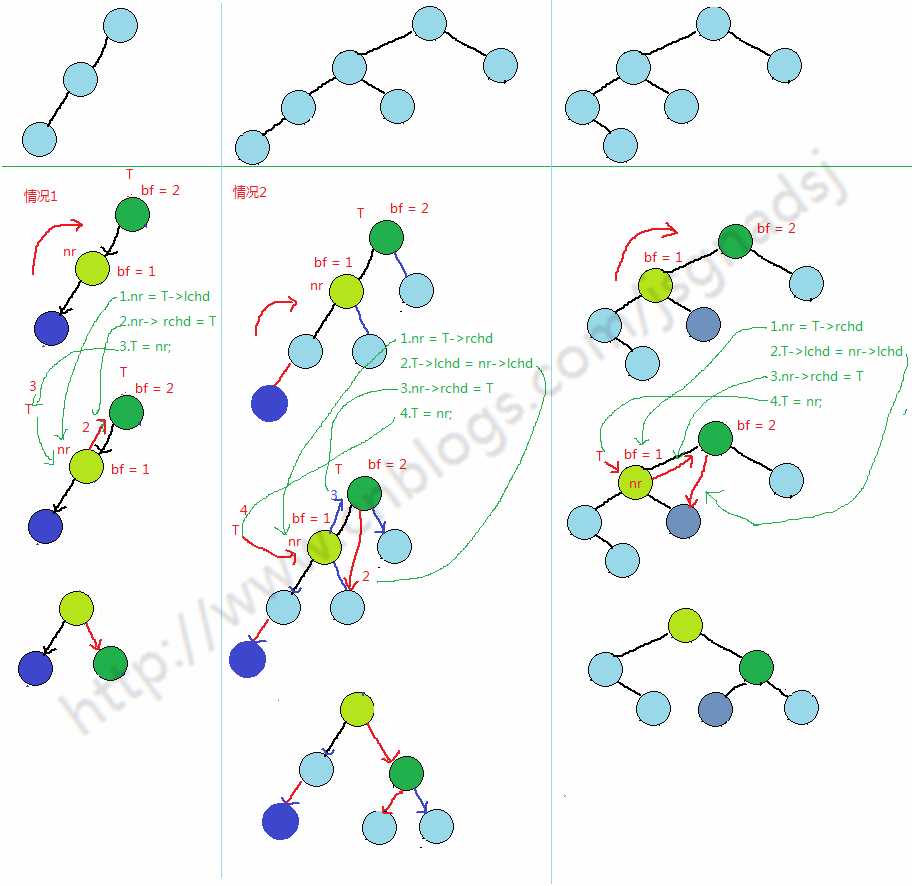
简单左右旋转代码:(只有一次)
void rotateL(pBinTree *p)//左旋转 { pBinTree r; r = (*p)->rchd; //r 为新的根 (*p)->rchd = r->lchd; r->lchd = (*p); (*p) = r; } void rotateR(pBinTree *p)//右旋转 { pBinTree r; r = (*p)->lchd; //r 为新的根 (*p)->lchd = r->rchd; //新根节点的右孩子附到旧的根结点的左孩子 r->rchd = (*p); (*p) = r; }
两次旋转 对应图中3(左右)情况
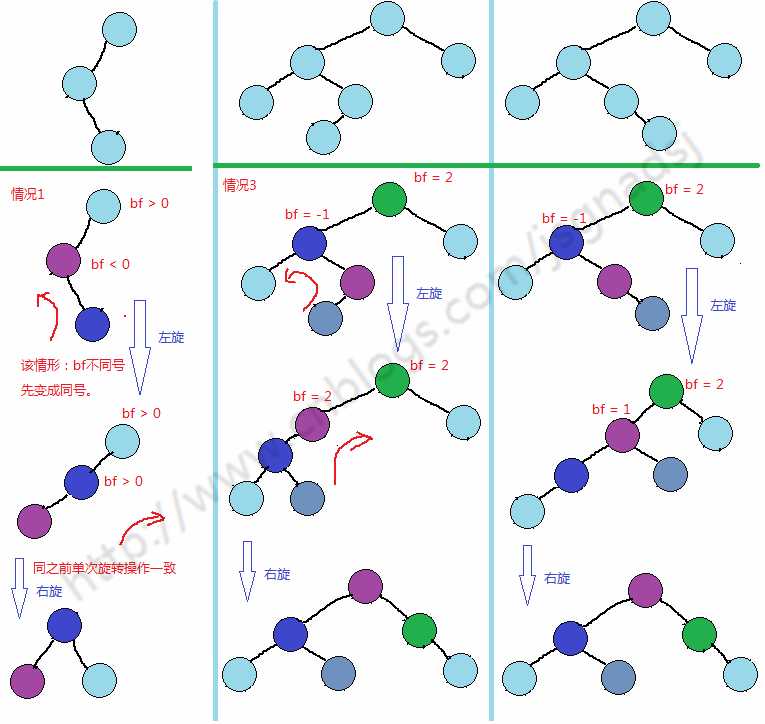
需要旋转两次简单的左右旋转。基于上面代码就可以实现。
为了方便,AVL引入了BF(平衡因子)来调整树。只要出现非平衡树就调整,把不平衡消除最小的情况。
下面就是通过判断BF来实现调整
void BlanceLeft(pBinTree *p)//从最小非平衡树开始调整 { pBinTree nR,nRchd; nR = (*p)->lchd; switch (nR->bf) { case LH: //新插入的结点在左子树 { (*p)->bf = EH; nR->bf = EH; rotateR(p); break; } case RH: //新插入的结点在右子树 { nRchd = nR->rchd; switch(nRchd->bf)//增加结点是nR的左孩子还是右孩子? { case LH:// { (*p)->bf = RH; nR->bf = EH; break; } case EH:// { (*p)->bf = EH; nR->bf = EH; break; } case RH: { (*p)->bf = EH; nR->bf = LH; break; } } nRchd->bf = EH; rotateL(&((*p)->lchd)); rotateR(p); } } } void BlanceRight(pBinTree *p)//从最小非平衡树开始调整 { pBinTree nR,nRchd; nR = (*p)->rchd; switch (nR->bf){ case RH: //新插入的结点在左子树 { (*p)->bf = EH; nR->bf = EH; rotateL(p); break; } case LH: //新插入的结点在右子树 { nRchd = nR->lchd; switch(nRchd->bf)//增加结点是nR的左孩子还是右孩子? { case LH:// { (*p)->bf = EH; nR->bf = RH; break; } case EH:// { (*p)->bf = EH; nR->bf = EH; break; } case RH: { (*p)->bf = LH; nR->bf = EH; break; } } nRchd->bf = EH; rotateR(&((*p)->rchd)); rotateL(p); } } }
然后再就是插入算法,这里采用递归的方式插入。
bool InsertAVL(pBinTree *T,int key,bool *taller) { if (!*T) { *T = (pBinTree)malloc(sizeof(BinTree)); (*T)->data = key; (*T)->bf = EH; 8 (*T)->lchd = NULL; (*T)->rchd = NULL; *taller = true; } else { if (key == (*T)->data) { *taller = false; return false; } if (key < (*T)->data) { if (!InsertAVL(&((*T)->lchd),key,taller)) { return false; } if (*taller) { switch ((*T)->bf) { case LH: { BlanceLeft(T); *taller = false; break; } case EH: { (*T)->bf = LH; *taller = true; break; } case RH: { (*T)->bf = EH; *taller = false; break; } } } } else // key > (*T)->data { if (!InsertAVL(&((*T)->rchd),key,taller)) { return false; } if (*taller) { switch ((*T)->bf) { case LH: { (*T)->bf = EH; *taller = false; break; } case EH: { (*T)->bf = RH; *taller = true; break; } case RH: { BlanceRight(T); *taller = false; break; } } } } } return true; }
以上的代码用switch case 显得非常的繁琐。会导致删除结点的程序判断BF调整非平衡的步骤更多。
以后添加删除部分代码。
完整代码:
// AVL.cpp : 定义控制台应用程序的入口点。 // #include "stdafx.h" #include #define LH 1 #define EH 0 #define RH -1 typedef int dataType; typedef struct BinTNode { dataType data; int bf; struct BinTNode *lchd,*rchd; }BinTree,*pBinTree; void rotateL(pBinTree *p) { pBinTree r; r = (*p)->rchd; //r 为新的根 (*p)->rchd = r->lchd; r->lchd = (*p); (*p) = r; } void rotateR(pBinTree *p) { pBinTree r; r = (*p)->lchd; //r 为新的根 (*p)->lchd = r->rchd; //新根节点的右孩子附到旧的根结点的左孩子 r->rchd = (*p); (*p) = r; } void BlanceLeft(pBinTree *p)//从最小非平衡树开始调整 { pBinTree nR,nRchd; nR = (*p)->lchd; switch (nR->bf) { case LH: //新插入的结点在左子树 { (*p)->bf = EH; nR->bf = EH; rotateR(p); break; } case RH: //新插入的结点在右子树 { nRchd = nR->rchd; switch(nRchd->bf)//增加结点是nR的左孩子还是右孩子? { case LH:// { (*p)->bf = RH; nR->bf = EH; break; } case EH:// { (*p)->bf = EH; nR->bf = EH; break; } case RH: { (*p)->bf = EH; nR->bf = LH; break; } } nRchd->bf = EH; rotateL(&((*p)->lchd)); rotateR(p); } } } void BlanceRight(pBinTree *p)//从最小非平衡树开始调整 { pBinTree nR,nRchd; nR = (*p)->rchd; switch (nR->bf){ case RH: //新插入的结点在左子树 { (*p)->bf = EH; nR->bf = EH; rotateL(p); break; } case LH: //新插入的结点在右子树 { nRchd = nR->lchd; switch(nRchd->bf)//增加结点是nR的左孩子还是右孩子? { case LH:// { (*p)->bf = EH; nR->bf = RH; break; } case EH:// { (*p)->bf = EH; nR->bf = EH; break; } case RH: { (*p)->bf = LH; nR->bf = EH; break; } } nRchd->bf = EH; rotateR(&((*p)->rchd)); rotateL(p); } } } bool InsertAVL(pBinTree *T,int key,bool *taller) { if (!*T) { *T = (pBinTree)malloc(sizeof(BinTree)); (*T)->data = key; (*T)->bf = EH; (*T)->lchd = NULL; (*T)->rchd = NULL; *taller = true; } else { if (key == (*T)->data) { *taller = false; return false; } if (key < (*T)->data) { if (!InsertAVL(&((*T)->lchd),key,taller)) { return false; } if (*taller) { switch ((*T)->bf) { case LH: { BlanceLeft(T); *taller = false; break; } case EH: { (*T)->bf = LH; *taller = true; break; } case RH: { (*T)->bf = EH; *taller = false; break; } } } } else // key > (*T)->data { if (!InsertAVL(&((*T)->rchd),key,taller)) { return false; } if (*taller) { switch ((*T)->bf) { case LH: { (*T)->bf = EH; *taller = false; break; } case EH: { (*T)->bf = RH; *taller = true; break; } case RH: { BlanceRight(T); *taller = false; break; } } } } } return true; } int _tmain(int argc, _TCHAR* argv[]) { int a[10] = {2,1,0,3,4,6,7,9,8,5}; int i; bool taller; pBinTree T = NULL; for (i=0;i<10;i++) { InsertAVL(&T,a[i],&taller); } getchar(); return 0; }
算法学习记录-查找——平衡二叉树(AVL),布布扣,bubuko.com
原文:http://www.cnblogs.com/wuchanming/p/3806327.html