1.线性最小二乘法
2.多项式拟合方法(polyfit)
3.最小二乘优化:lsqlin,lsqcurvefit,lsqnonlin,lsqnonneg
4.曲线拟合的用户图形界面求法(cftool)


x=[19 25 31 38 44]‘; y=[19.0 32.3 49.0 73.3 97.8]‘; r=[ones(5,1),x.^2]; ab=r\y % if AB=C then B=A\C x0=19:0.1:44; y0=ab(1)+ab(2)*x0.^2; plot(x,y,‘o‘,x0,y0,‘r‘)
运行结果:
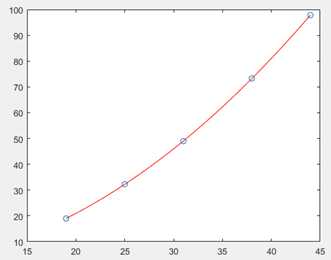
2. 多项式拟合方法

x0=[1990 1991 1992 1993 1994 1995 1996]; y0=[70 122 144 152 174 196 202]; a=polyfit(x0,y0,1) y97=polyval(a,1997) x1=1990:0.1:1997; y1=a(1)*x1+a(2); plot(x1,y1) hold on plot(x0,y0,‘*‘) plot(1997,y97,‘o‘)
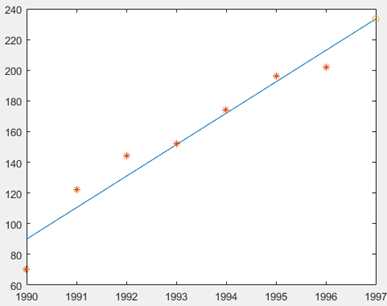
3.1 lsqlin 函数
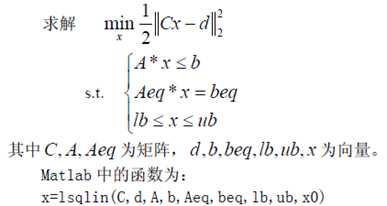
例四:
x=[19 25 31 38 44]‘; y=[19.0 32.3 49.0 73.3 97.8]‘; r=[ones(5,1),x.^2]; ab=lsqlin(r,y) x0=19:0.1:44; y0=ab(1)+ab(2)*x0.^2; plot(x,y,‘o‘,x0,y0,‘r‘)
3.2 lsqcurvefit 函数
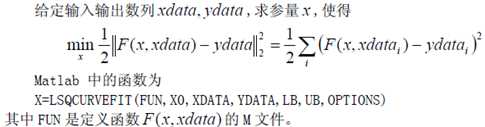
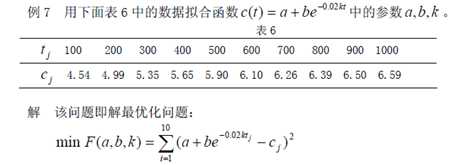
(1)定义函数
function f=fun1(x,tdata);
f=x(1)+x(2)*exp(-0.02*x(3)*tdata); %其中x(1)=a,x(2)=b,x(3)=k
(2)主函数
td=100:100:1000; cd=[4.54 4.99 5.35 5.65 5.90 6.10 6.26 6.39 6.50 6.59]; x0=[0.2 0.05 0.05]; x=lsqcurvefit(@fun1,x0,td,cd) % x(1)=a,x(2)=b,x(3)=k t=100:10:1000; c=x(1)+x(2)*exp(-0.02*x(3)*t); plot(t,c) hold on plot(td,cd,‘*‘
3.3 lsqnonlin 函数
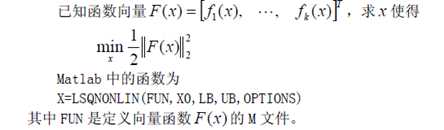
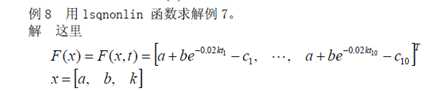
(1)定义函数
function f=fun2(x); td=100:100:1000; cd=[4.54 4.99 5.35 5.65 5.90 6.10 6.26 6.39 6.50 6.59]; f=x(1)+x(2)*exp(-0.02*x(3)*td)-cd;
(2)主函数
x0=[0.2 0.05 0.05]; %初始值是任意的
x=lsqnonlin(@fun2,x0)
3.4 lsqnonneg 函数


c=[0.0372 0.2869;0.6861 0.7071;0.6233 0.6245;0.6344 0.6170]; d=[0.8587;0.1781;0.0747;0.8405]; x=lsqnonneg(c,d)
Matlab 工具箱提供了命令cftool,该命令给出了一维数据拟合的交互式环境。具体
执行步骤如下:
(1)把数据导入到工作空间;
(2)运行cftool,打开用户图形界面窗口;
(3)对数据进行预处理;
(4)选择适当的模型进行拟合;
(5)生成一些相关的统计量,并进行预测。
原文:http://www.cnblogs.com/youngsea/p/7501786.html