csapp page124. practice problem 2.35
/* Determine whether arguments can be multiplied without overflow */
int tmult_ok(int x, int y){
int p = x*y;
/* Either x is zero, or dividing p by x gives y */
return !x || p/x == y;
}
函数 tmult_ok 的功能是检查两个二补数相乘会不会溢出, 逻辑是,要么 x 为零, 或者 乘积 p 除以 x 等于另一个乘数 y 的话,就说明不会溢出。
这题要求给出这个函数正确性的数学证明。首先证明当x=0这个情况的正确性。然后考虑w位的数字(w不等于0) 有 y, p, 和 q, 其中 p 是x, y执行了二补码乘法后的结果, q 是 p/x 的值。
书中给出三条线索,分别给出这三条线索的证明即可证明这个函数的正确性。
答案是这么证明的:
1.因为x,y都是w位二补码表示的数,所以他们的乘积最多要用2w位表示,因为:
-2^(w-1) <= x, y <=2^(w-1) - 1 注:这是二补码的取值范围
所以 x*y 就要 大于等于 -2^(w-1) * (2^(w-1) - 1) 就等于 -2^(2*w - 1) + 2^(w - 1) 注: 其实就是Tmax*Tmin
小于等于 (-2^(w - 1))^2 就等于 2^(2*w - 2) 注: 其实就是Tmin*Tmin,可以证明Tmax^2 没有 Tmin^2大
看见2的次方数是2w起跳的,就说明肯定得要2w位才能表示了。所以 x*y 理应是要用 2w 位表示的(但是2w位是溢出的,暂时不管),现在设 u 等于该乘积低w位的无符号形式,v 等于该乘积高w位的二补码形式。
那么,根据公式2.3 即二进制到二补码的转换公式可以得出 x*y = v*2^w + u 这个式子乍一看匪夷所思,怎么能把一个位向量劈成两半,前w位按二补码算然后乘以2^w ,后w位按无符号算然后两个部分加起来怎么刚好就是x和y的乘积??
其实只要根据二进制转二补码的公式细心推倒,马上就可以证明这个结论:
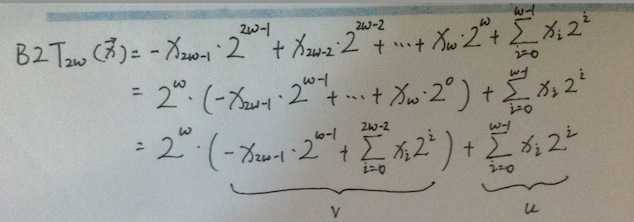
我们还知道 u = T2U(p) 这里p是二补码乘积,因为实际上不管乘积结果有没有溢出,unsigned形式和tow‘s complement形式的乘积在w位上是一模一样的,这点在数的2.18给出了证明。
所以根据公式T2U 得 u = pw-1 * 2^w + p, 把u 带入之前的 x*y = v*2^w + u 这里, 化简可以得到: x*y = 2^w * (v + pw-1) + p, 此时我们设 t = v + pw-1,公式变为:x*y = t* 2^w + p
这里我们就可以看出,当且仅当 t = 0 的时候, x*y 才等于p,t 不等于 0 的时候乘积是溢出的。到这里证明了上面的第1条。
2.因为无论 x*y 的值 p 有没有溢出,总之它是个整数,那么只要 p 是个整数,它除以一个非零整数 x 必然会得到一个商(q)和一个余数(r) 使得 p = x * q + r 其中 |r| < |x|
这里取绝对值是因为r 和 x 的符号可能不一样,比如 -7 / 2 得 -3 余 -1, |-1| < |2|。 这里证明了第2条。
3. 如果 q = y 根据 p = x*q+r 得出 p = x*y+r 其中 x*y = t * 2^w + p 所以 p = t*2^w + p + r, 两边消去 p 以后得到 t*2^w = -r 要让这个等式成立,有两种情况,要么等号两边值相等,要么两边都为零。
在第2条的证明中,我们得出 |r| < |x|, 而x是二补码,所以绝对值的最大值是 2^w 所以 |r| < 2^w, 回到这里,等式左边出现了2^w 而 r 要比2^w 小,可见其值必不相等,则必须是为零的情况。所以必须 r = t = 0
根据第1条证明,我们知道要想乘积不溢出,t 必须为 0, 根据第三条,当且仅当 t 为 0 的时候 p / x = y 用程序表示就是 (!x || p / x == q) 这个逻辑被证明是正确的。
这样3也证明了,再看x=0的情况,x等于零的时候乘积为零肯定不会溢出嘛,所以这个程序是正确可靠的。证毕。
原文:http://www.cnblogs.com/agentgamer/p/3807054.html