在社交网络(social network)的研究中,我们常常使用图论概念去解释一些社会现象。不妨看这样的一个问题。在一个社交圈子里有n个人,人与人之间有不同程度的关系。我 们将这个关系网络对应到一个n个结点的无向图上,两个不同的人若互相认识,则在他们对应的结点之间连接一条无向边,并附上一个正数权值c,c越小,表示两 个人之间的关系越密切。
我们可以用对应结点之间的最短路长度来衡量两个人s和t之间的关系密切程度,注意到最短路径上的其他结点为s和t的联系提供了某种便利, 即这些结点对于s 和t之间的联系有一定的重要程度。我们可以通过统计经过一个结点v的最短路径的数目来衡量该结点在社交网络中的重要程度。
考虑到两个结点A和B之间可能会有多条最短路径。我们修改重要程度的定义如下:
令Cs,t表示从s到t的不同的最短路的数目,Cs,t(v)表示经过v从s到t的最短路的数目;则定义
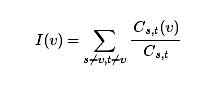
为结点v在社交网络中的重要程度。
为了使I(v)和Cs,t(v)有意义,我们规定需要处理的社交网络都是连通的无向图,即任意两个结点之间都有一条有限长度的最短路径。
现在给出这样一幅描述社交网络s的加权无向图,请你求出每一个结点的重要程度。
输入格式:
输入第一行有两个整数,n和m,表示社交网络中结点和无向边的数目。在无向图中,我们将所有结点从1到n进行编号。
接下来m行,每行用三个整数a, b, c描述一条连接结点a和b,权值为c的无向边。注意任意两个结点之间最多有一条无向边相连,无向图中也不会出现自环(即不存在一条无向边的两个端点是相同的结点)。
输出格式:
输出包括n行,每行一个实数,精确到小数点后3位。第i行的实数表示结点i在社交网络中的重要程度。
4 4 1 2 1 2 3 1 3 4 1 4 1 1
1.000 1.000 1.000 1.000
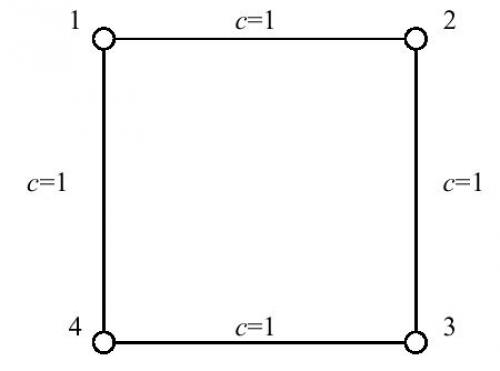
对于1号结点而言,只有2号到4号结点和4号到2号结点的最短路经过1号结点,而2号结点和4号结点之间的最短路又有2条。因而根据定义,1号结点的重要程度计算为1/2+1/2=1。由于图的对称性,其他三个结点的重要程度也都是1。
50%的数据中:n ≤10,m ≤45
100%的数据中:n ≤100,m ≤4 500,任意一条边的权值c是正整数,满足:1 ≤c ≤1 000。
所有数据中保证给出的无向图连通,且任意两个结点之间的最短路径数目不超过10^10。
进行两次floyed
第一次算出最短路和方案数
实现方法dis[i][j]==dis[i][k]+dis[k][j]时
d[i][j]+=d[i][k]*d[k][j]
第二次算出答案
枚举断点
ans=∑d[i][k]*d[k][j]/d[i][j]
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<queue> 6 using namespace std; 7 typedef long long ll; 8 ll n,m,dis[201][201]; 9 ll d[201][201]; 10 double s; 11 int main() 12 { 13 ll i,u,v,c,j,k; 14 cin>>n>>m; 15 memset(dis,127/3,sizeof(dis)); 16 for (i=1; i<=m; i++) 17 { 18 scanf("%lld%lld%lld",&u,&v,&c); 19 if (dis[u][v]>c) 20 { 21 dis[u][v]=dis[v][u]=c; 22 d[u][v]=d[v][u]=1; 23 } 24 else if (dis[u][v]==c) d[u][v]=++d[v][u]; 25 } 26 for (k=1;k<=n;k++) 27 { 28 for (i=1;i<=n;i++) 29 { 30 for (j=1;j<=n;j++) 31 if (i!=k&&i!=j&&k!=j) 32 if (dis[i][k]+dis[k][j]<dis[i][j]) 33 { 34 dis[i][j]=dis[i][k]+dis[k][j]; 35 d[i][j]=d[i][k]*d[k][j]; 36 } 37 else if (dis[i][k]+dis[k][j]==dis[i][j]) 38 { 39 d[i][j]+=d[i][k]*d[k][j]; 40 } 41 } 42 } 43 for (i=1; i<=n; i++) 44 { 45 s=0; 46 for (j=1; j<=n; j++) 47 { 48 for (k=1; k<=n; k++) 49 if (i!=j&&j!=k&&i!=k&&dis[j][i]+dis[i][k]==dis[j][k]) 50 s+=(double)d[j][i]*d[i][k]/(double)d[j][k]; 51 } 52 printf("%.3lf\n",s); 53 } 54 }
原文:http://www.cnblogs.com/Y-E-T-I/p/7594243.html