刚开始拿到题目后,看到要求上写着:
完成一个能自动生成小学四则运算题目的命令行 “软件”
首先想到的是用rand()函数生成操作数和运算符,然后先从简单地只生成两个操作数的四则运算式,并且只考虑整数之间的运算。实现前面一步,再看题目运算符要求三个以上,这就需要用数组来存放操作数和运算符,同样很容易能随机生成多个操作数的四则运算式。接着遇到了最困难的一步:
要求能处理用户的输入,并判断对错,打分统计正确率。
要能判断用户输入的对错就必须计算四则运算式的结果,一开始想到既然操作数和运算符都存放在数组里了,那么直接遍历数组,根据操作符将操作数取出计算。结果发现由于需要考虑运算的优先级,用数组操作过程极为复杂,很难计算出正确结果。于是从网上查找资料,发现用后缀表达式计算四则运算算法思路简单清晰。共需要准备三个容器,符号栈operatorStack,数字栈numStack和盛放后缀表达式的队列expQueue。按照下列的规则进行:
由于对栈和队列的操作不够熟练,并且以上只用到了基本操作,所以决定用数组来代替栈和队列,通过下标变换可以实现同样的效果。不过又遇到一个问题,那就是盛放后缀表达式的expQueue数组需要同时存放操作数和运算符,两者类型不同无法用数组存放。经过尝试,想出一个方法那就是:把操作数单独存放到数组里面,而在expQueue中存放该操作数对应的下标。完成以上功能后,还需解决题目的最后一个需求:
参与运算的操作数(operands)除了100以内的整数以外,还要支持真分数的四则运算,例如:1/6 + 1/8 = 7/24。
看到这个要求,一时之间又遇到了难题:一个真分数需要考虑分子和分母两个操作数,如果支持真分数的四则运算,那么不如把所有操作都想转换成分数,最后对结果进行化简,那么问题就转化为如何处理两个分数的运算?经过反复思考,想到一个令自己比较满意的解决方法,那就是使用结构体,定义两个成员变量分别代表分子、分母。完成以上的设计分析再开始编程,发现代码的编写十分顺利!
基本功能
1.返回操作符的优先级

int mPriority(char op){ if(op==‘+‘) return 1; else if(op==‘-‘) return 1; else if(op==‘x‘) return 2; else if(op==‘%‘) return 2; }
2.求最大公约数

int gcd(int a,int b) { if(b==0) return a; else return gcd(b,a%b); }
3.根据操作符计算两个操作数

Digit Calculate(Digit num1,Digit num2,char op){ Digit res; int f; //根据运算符,作两个分数之间的四则运算 switch(op){ case ‘+‘:{ res.x=num1.x*num2.y+num1.y*num2.x; res.y=num1.y*num2.y; break; } case ‘-‘:{ res.x=num1.x*num2.y-num1.y*num2.x; res.y=num1.y*num2.y; break; } case ‘x‘:{ res.x=num1.x*num2.x; res.y=num1.y*num2.y; break; } case ‘%‘:{ res.x=num1.x*num2.y; res.y=num1.y*num2.x; break; } default:{ res.x=0; res.y=1; } } if(res.x<res.y) f=gcd(res.y,res.x); else f=gcd(res.x,res.y); res.x=res.x/f;res.y=res.y/f; //如果分母为负数,取反 if(res.y<0){ res.x=-res.x; res.y=-res.y; } return res; }
4.随机生成1个操作数并打印

Digit getNum() { int i,j,f; Digit res; if(rand()%3==1)//1/3的概率生成一个真分数 { i=rand()%11+1; j=rand()%11+1; if(i>j) {int temp=i;i=j;j=temp;} f=gcd(j,i); i=i/f;j=j/f; printf("%d/%d",i,j); }else{ i=rand()%101+1; j=1; printf("%d",i); } res.x=i; res.y=j; return res; }
5.随机生成一个操作符并打印

char getOperator(){ char op=ss[rand()%4]; //打印操作符 if(op==‘%‘) printf("÷"); else if(op==‘x‘) printf("×"); else printf("%c",op); return op; }
主函数

int main() { srand((unsigned)time(NULL)); //每次运行进行初始化 int times; //控制生成题目的个数 float score=100; //题目得分 scanf("-n %d",×); printf("本次共%d题,满分100分\n",times); //第一个for循环,每次生成一个题目 for(int j=0;j<times;j++){ printf("%d: ",j+1); int t=0,q=0,p=0,top=0; Digit opNum[10],numStack[10]; char op,operatorStack[10],expQueue[20]; opNum[q++]=getNum(); expQueue[p++]=q-1+‘0‘; //得到后缀表达式 for(t=0;t<3;t++) { op=getOperator(); if(t==0){ operatorStack[top++]=op; opNum[q++]=getNum(); expQueue[p++]=q-1+‘0‘; continue; } while(mPriority(op)<=mPriority(operatorStack[top-1])&&top>0){ top--; expQueue[p++]=operatorStack[top]; } opNum[q++]=getNum(); expQueue[p++]=q-1+‘0‘; operatorStack[top++]=op; } while(top>0){ top--; expQueue[p++]=operatorStack[top]; } //根据后缀表达式计算结果 top=0; for(int i=0;i<p;i++){ if(expQueue[i]>=‘0‘&&expQueue[i]<=‘9‘) { int ch=expQueue[i]-‘0‘; numStack[top].x=opNum[ch].x; numStack[top].y=opNum[ch].y; top++; }else{ top--; numStack[top-1]=Calculate(numStack[top-1],numStack[top],expQueue[i]); } } printf("="); //用户输入计算结果 char userAns[100],rightAns[100]; // printf("%d/%d\n",numStack[top-1].x,numStack[top-1].y); cin>>userAns; int c=getchar(); //得到的正确结果 if(numStack[top-1].y!=1){ sprintf(rightAns,"%d%s",numStack[top-1].x,"/"); sprintf(rightAns,"%s%d",rightAns,numStack[top-1].y); } else sprintf(rightAns,"%d",numStack[top-1].x); //printf("%s\n",rightAns); //判断对错 if(strcmp(userAns,rightAns)==0) printf("正确!\n"); else { printf("不正确!正确答案= %s\n",rightAns); //扣分 score-=100*1.0/times; } } printf("本次得分%.2f",score); return 0; }
上面代码只实现了基本功能,对于附加功能运算符个数随机生成,只需改变t的值即可。至于带括号的多元复合运算,整个代码的思路没有改变,特别对后缀表达式的计算部分不用作任何变动。在得到后缀表达式的过程,分别在运算符之后随机生成左括号,在合适的操作数之后生成相应的右括号,另外,需要在符号栈的进出栈作一些改变。对代码作改进的部分如下:

//加入附加功能,运算符个数随机生成 int op_Num=rand()%5+1; //附加功能,控制括号的生成 int braket_Max=2,braket=0,flag=0;//分别代表生成括号的个数和当前左括号个数 //得到后缀表达式 for(t=0;t<op_Num;t++) { op=getOperator(); //生成运算符 if(t==0){ operatorStack[top++]=op; //随机决定是否生成左括号 if(rand()%3==1&&t<op_Num-1){ printf("(");//打印括号 braket_Max--; braket++; operatorStack[top++]=‘(‘; //左括号入栈 } opNum[q++]=getNum(); expQueue[p++]=q-1+‘0‘; continue; } //当符号栈顶不是左括号,根据优先级判断出栈 if(operatorStack[top-1]!=‘(‘){ while(mPriority(op)<=mPriority(operatorStack[top-1])&&top>0&&operatorStack[top-1]!=‘(‘){ top--; expQueue[p++]=operatorStack[top]; } } operatorStack[top++]=op; //随机决定是否生成左括号 if(rand()%3==1&&t<op_Num-1){ if(braket_Max<0) break;//如果已经生成三对括号,就不再生成 printf("(");//打印括号 flag=t; braket_Max--; braket++; operatorStack[top++]=‘(‘; //左括号入栈 } opNum[q++]=getNum();//产生一个随机数 expQueue[p++]=q-1+‘0‘; //随机决定是否生成右括号 if(flag!=t&&rand()%3==1){ if(braket<=0) break; printf(")");//打印右括号 braket--; //一直出栈直到遇到左括号 while(operatorStack[top-1]!=‘(‘) { top--; expQueue[p++]=operatorStack[top]; } top--; } } //如果还有左括号还未匹配 while(braket>0){ braket--; printf(")"); while(operatorStack[top-1]!=‘(‘) { top--; expQueue[p++]=operatorStack[top]; } top--; } while(top>0){ top--; expQueue[p++]=operatorStack[top]; }
计算结果为分数可能在分母出现负号。
if(res.y<0){ res.x=-res.x; res.y=-res.y; }
还有各种小问题,就不一一叙述了。
根据需要在-n后面输入要生成的题目个数,每个运算式后面输入自己的计算结果,由程序自动判断对错。
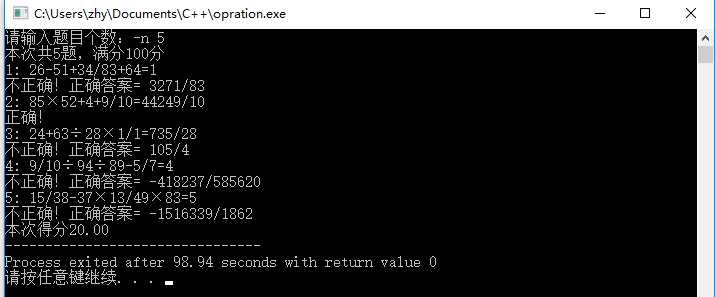
基本功能:
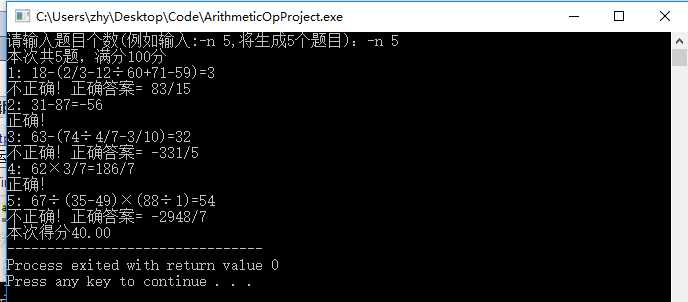
支持附加功能
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 10 | 5 |
| · Estimate | · 估计这个任务需要多少时间 | 10 | 5 |
| Development | 开发 | 600 | 695 |
| · Analysis | · 需求分析 (包括学习新技术) | 60 | 50 |
| · Design Spec | · 生成设计文档 | 10 | 30 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 10 | 10 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 5 |
| · Design | · 具体设计 | 120 | 300 |
| · Coding | · 具体编码 | 200 | 180 |
| · Code Review | · 代码复审 | 30 | 20 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 170 | 100 |
| Reporting | 报告 | 250 | 210 |
| · Test Report | · 测试报告 | 120 | 100 |
| · Size Measurement | · 计算工作量 | 30 | 20 |
| ·Postmortem& Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 100 | 90 |
| 合计 | 860 | 910 |
第一次做软件工程项目,虽然是一个小项目,但是也学到了软件开发的一部分流程。体会比较深的就是,在开发的过程中把更多的时间投入的开发设计和测试上,而不是把重点放在代码的编写上。用更多的时间构思,把程序需要解决的问题考虑清楚,这样写起代码思路十分清晰,不会出现代码混乱,确实提高了开发效率。另外,通过这次作业学习了GitHub的基本用法,知道了如何使用GitHub管理自己的项目,给自己的开发有很大的帮助。
原文:http://www.cnblogs.com/yundanzhy/p/7586729.html