此次比赛为厦门一中出题。都是聚劳,不敢恭维。
莫名爆了个0,究其原因,竟然是快读炸了……很狗,很难受。
话不多说,来看看题:
【T1】
题意:

样例:
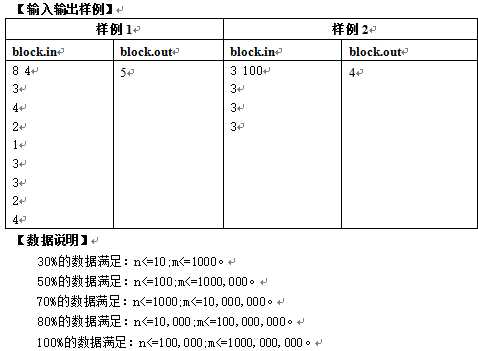
PS:1<=h[i]<=100000。
题解:
假设\(max\left(h_{i}\right)=M\),可以发现最大高度不超过\(M+n\)。
而用\(m\)块砖,向上最多能搭\(\sqrt{m}\)个。
故最大高度为\(M+min\left(n,\sqrt{m}\right)\)。
而最低高度为\(M\)(或\(M+1\))。
也就是说,高度的范围不超过3163。
而可以看出对于高度\(h\),能否搭建起高\(h\)的塔是单调的。
如果我们二分高度\(h\),计算能否搭建,就能够较快出解。
考虑在第\(i\)列搭上\(h\)的高度,那么最少需要多少砖块呢?
当然是按照金字塔形斜向下,直到遇到第一个可以作为支撑的砖块。
设\(left\left[i\right]\left[h\right]\)为坐标\(\left(i,h\right)\)向左斜向下遇到的第一个砖块的标号,\(right\left[i\right]\left[h\right]\)则为向右斜向下,若不存在,则值为0。
那么最少需要的砖块数(包括已经搭建的)等于:
\(Sum[i][h]=h(right[i][h]-left[i][h]-1)-\frac{(i-left[i][h])(i-left[i][h]-1)}{2}-\frac{(right[i][h]-i)(right[i][h]-i-1)}{2}\)。
而需要多搭的为:\(Sum[i][h]-(sum_{right[i][h]-1}-sum_{left[i][h]})\),其中\(sum\)为前缀和。
现在,如何快速算出\(left\)和\(right\)呢?
看往左斜向下的,容易发现,\(k\)能够阻挡\((i,h)\)当且仅当\(h_{k}-k\geqslant h-i\)。
而对于向右下方的,我们有,\(k\)能够阻挡\((i,h)\)当且仅当\(h_{k}+k\geqslant h+i\)。
【四校联考】【比赛题解】FJ NOIP 四校联考 2017 Round 7
原文:http://www.cnblogs.com/PinkRabbit/p/7618236.html