http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1624
题意: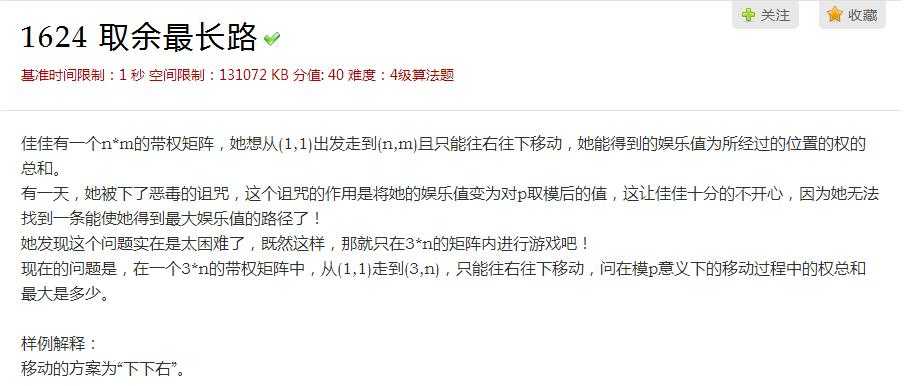
思路:
因为一共只有3行,所以只需要确定第一行和第二行的转折点就行,如果是暴力枚举的话,时间复杂度会比较高,为了降低时间复杂度,可以采用枚举第一行,然后二分第二行的方法来做。
设sum(i,l,r)表示第i行从l到r元素的和,则答案可以表示为sum(1,1,x)+sum(2,x,y)+sum(3,y,n)%p。
前缀和一下转化成(S3[n]-S3[y-1])+S2[y]+(S1[x]-S2[x-1])%p,从小到大枚举y,将所有(S1[x]-S2[x-1])扔到一个集合里,用个set就能轻松实现了。
1 #include<iostream> 2 #include<algorithm> 3 #include<cstring> 4 #include<cstdio> 5 #include<vector> 6 #include<stack> 7 #include<queue> 8 #include<cmath> 9 #include<map> 10 #include<set> 11 using namespace std; 12 typedef long long ll; 13 typedef pair<int,int> pll; 14 const int INF = 0x3f3f3f3f; 15 const int maxn = 100000+5; 16 17 int n, p; 18 ll sum[4][maxn]; 19 20 int main() 21 { 22 //freopen("in.txt","r",stdin); 23 while(~scanf("%d%d",&n,&p)) 24 { 25 sum[1][0]=sum[2][0]=sum[3][0]=0; 26 for(int i=1;i<=3;i++) 27 { 28 for(int j=1;j<=n;j++) 29 { 30 int x; scanf("%d",&x); 31 sum[i][j]=(sum[i][j-1]+x)%p; 32 } 33 } 34 set<int> s; 35 ll ans = 0; 36 for(int i=1;i<=n;i++) 37 { 38 ll tmp = (sum[1][i]-sum[2][i-1]+p)%p; 39 s.insert(tmp); 40 tmp=(sum[2][i]-sum[3][i-1]+sum[3][n]+p)%p; 41 set<int>::iterator it = s.lower_bound(p-tmp); 42 if(it!=s.begin()) 43 ans=max(ans,tmp+*(--it)); 44 } 45 printf("%lld\n",ans); 46 } 47 return 0; 48 }
原文:http://www.cnblogs.com/zyb993963526/p/7633234.html