哈夫曼树
种根据我已刷的初赛题中基本每套的倒数第五或第六个不定项选择题就有一个关于哈夫曼树及其各种应用的题,占:0—1.5分;然而我针对这个类型的题也多次不会做,so,今晚好好研究下哈夫曼树;
给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。
————维基百科
自己结合维基百科和dalao的博客大致理解了下概念:就是一颗最优的二叉树,从根节点到需要到达的节点的权值之和最小,即为最优,举个例子:
一个很简单的程序,根据输入的分数判断等级,一共有五个等级,其主要的判断算法是这样的:
if(score<60) cout<<"E"<<endl; else if(score<70) cout<<"D"<<endl else if(score<80) cout<<"C"<<endl; else if(score<90) cout<<"B"<<endl; else cout<<"A!"<<endl;
用一个二叉树来表示是这样的: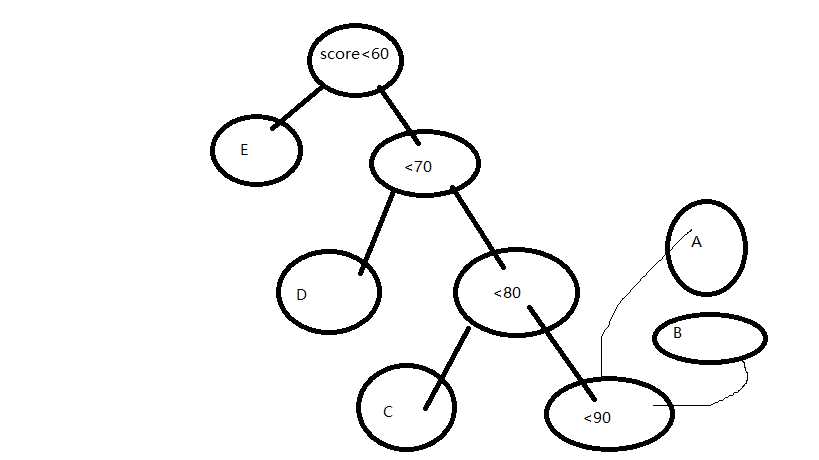
【原谅我;灵魂画师】
可以很明显得看出,这种方式的效力是非常低下的,N的最差情况要比较四次,如果等级划分更严密的话【比如划分100000000000个等级】,这种方式明显TLE;
因此,我们可以采用哈夫曼树的思想: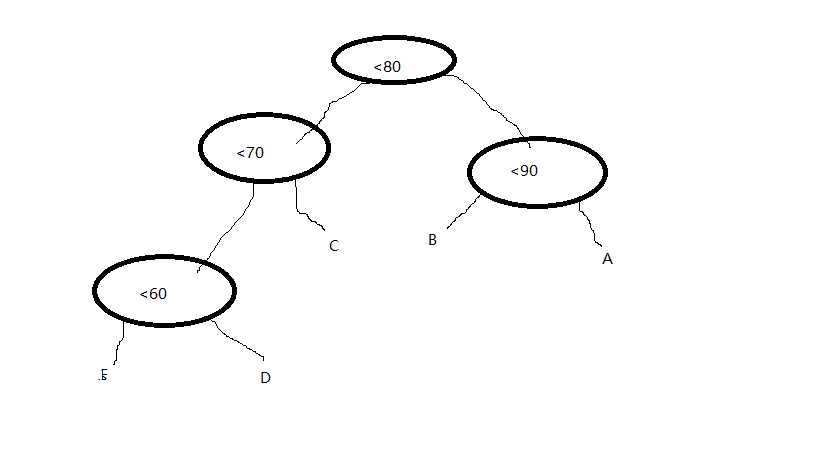
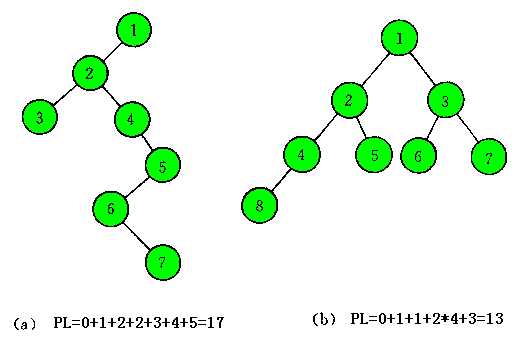
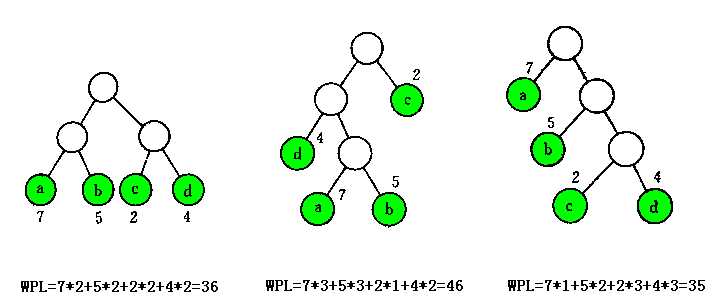
例如例1,构造哈夫曼树的WPL为35是最小的。具体比较如下图:
原文:http://www.cnblogs.com/akenderman/p/7635897.html