1. 选择排序
(1)基本思想:每次(例如第i次,i=1,2,…,n-2)从后面n-i个待排的数据元素中选出关键字最小的元素,作为有序元素序列第i个元素。
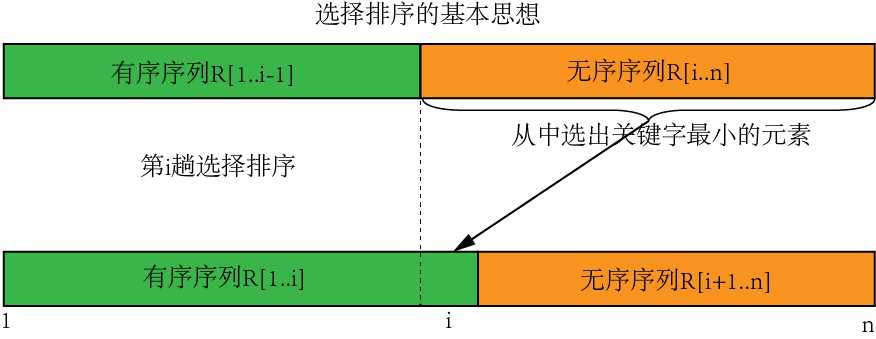
(2)实例分析
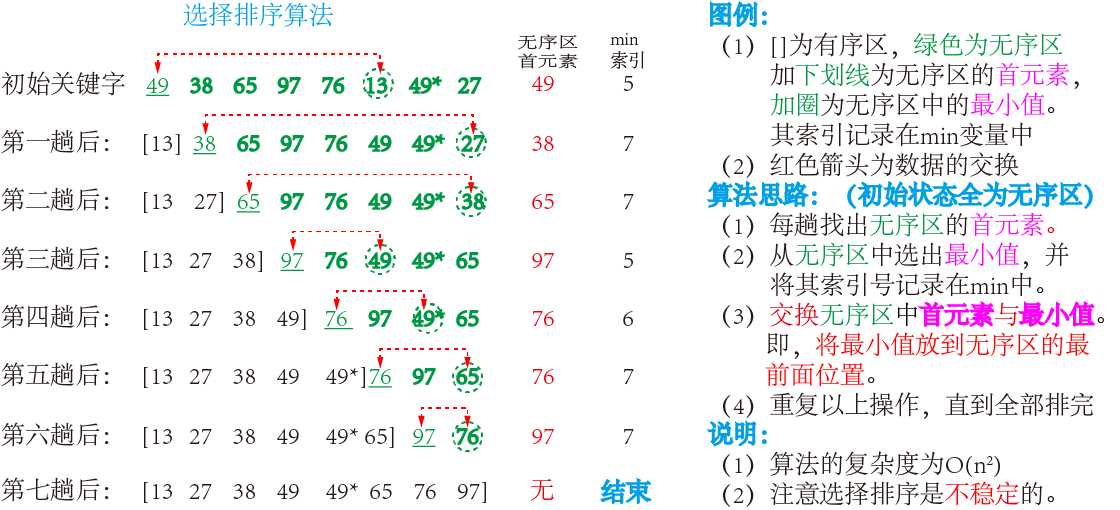
2. 插入排序
(1)插入排序的基本思想
当插入第i(i≥1)个数据元素时,前面的V[0],V[1],…,V[i-1]已经排好序;这时,用V[i]的关键字与v[i-1],v[i-2],…,V[0]的关键字进行比较,找到位置后将V[i]插入,原来位置上的对象向后顺移。
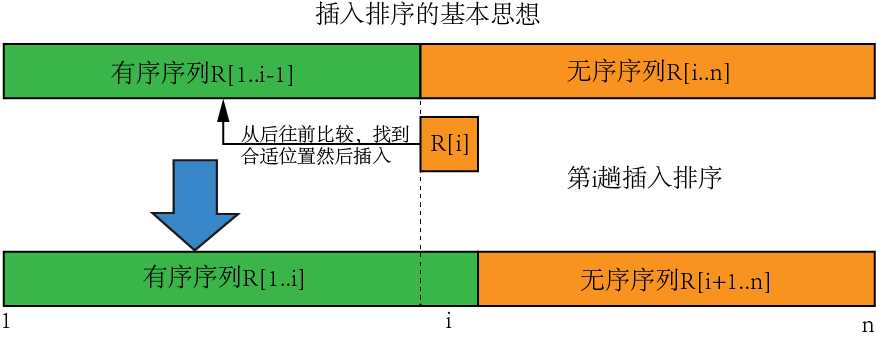
(2)实例分析

【编程实验】选择排序(Sort::select)和插入排序(Sort::Insert)的实现
//Sort.h
#ifndef SORT_H #define SORT_H #include "Object.h" namespace DTLib { class Sort : public Object { private: //私有化构造函数、赋值、拷贝构造等函数 Sort(); Sort(const Sort&); Sort& operator=(const Sort&); template <typename T> static void Swap(T& a, T& b) { T temp(a); a = b; b = temp; } public: //选择排序(O(n*n),不稳定) template <typename T> static void Select(T array[], int len, bool min2max = true) { for(int i=0; i<len-1; i++){ //第i趟。有序区为[0,i-1],无序区为[i, len-1] //1.找到无序区的首元素: array[i] //2.从无序区中找到最小值 int min = i; //假设:无序区中最小元素的为首元素 for(int j=i+1; j<len; j++){ if (min2max ? (array[j] < array[min]) : (array[j] > array[min])){ min = j; } } //3. 交换无序区中首元素和最小值的位置,将最小值放在无序区的首部 if(i != min){ Swap(array[i], array[min]); } } } //插入排序(O(n*n), 稳定) template <typename T> static void Insert(T array[], int len, bool min2max = true) { //1. 初始状态有序区为[0],无序区为[1..n-1] for(int i=1; i<len; i++){ //注意,从1开始,因为要将无序区的每个元素插入到有序区中 //有序区[0, i-1],无序区[i, n-1] //2. 取出无序区首元素,从有序区后面往前面比较依次与其比较 T e = array[i]; //无序区首元素 int k = i; //k记录着e最终应该放置的位置 for(int j=i-1; (j>=0) && (min2max ? (e<array[j]) : (e>array[j]));j--){ //3. 边比较边移动元素,e最终的位置记录在k中 array[j+1] = array[j]; //将a[j]往后移一位 k = j; } //4. 将e放置下来 if(k != i){ array[k] = e; } } } }; } #endif // SORT_H
//main.cpp
#include <iostream> #include "Sort.h" using namespace std; using namespace DTLib; int main() { int array[]={49,38,65,97,76,13,49,27}; int len = sizeof(array)/sizeof(*array); Sort::Insert(array, len,false);//降序排序 for(int i=0; i<len; i++){ cout << array[i] << " "; } cout << endl; return 0; } /*测试结果 97 76 65 49 49 38 27 13 */
3. 小结
(1)选择排序每次选择未排元素中的最小元素。
(2)插入排序每次将第i个元素插入到前面i-1个己排元素中。
(3)选择排序是不稳定的排序法,插入排序是稳定的排序方法
(4)选择排序和插入排序的时间复杂度为O(n2)
原文:http://www.cnblogs.com/5iedu/p/7643335.html